Singulärwertzerlegung
• svds(A) – Gibt einen Vektor zurück, der die singulären Werte von A, die positiven Quadratwurzeln der eigenvalues von Matrix AH·A enthält, wobei AH die konjugierte Transponiert von A ist. AH mit Hilfe der Operatoren transpose und complex conjugate wie folgt berechnen.
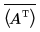
• svd(A) – Gibt einen Vektor mit drei verschachtelten Arrays zurück.
Das erste Array enthält den Vektor s der von svds zurückgegebenen singulären Werte. Die beiden folgenden Arrays sind die Matrizen U und VH, die A = U∙diag(s)·VH entsprechen. Der dritte Eintrag VH ist die konjugierte Transponierte von V .
Das dritte Array ist VH und nicht V. Dies bedeutet, dass die konjugierte Transponierte bereits auf das zurückgegebene Array angewendet wurde. Sie müssen sie nicht erneut anwenden. Sie können das zurückgegebene Array direkt in der Formel verwenden.
Argumente
• A ist ein m × n Array, wobei m ≥ n. Für svd müssen die Arrayelemente reelle Zahlen sein, für svds sind komplexe Werte zulässig.
Zusätzliche Informationen
• Singuläre Werte sind stets reell und positiv. Sehr kleine Werte müssen als 0 interpretiert werden.
• Die Funktion svd verwendet die Bibliotheken Intel Basic Linear Algebra Subprograms (BLAS)/Linear Algebra Package (LAPACK).