Beispiel: SVD-Matrixfaktorisierung
Verwenden Sie die Funktion svd, um eine SVD-Matrixfaktorisierung durchzuführen. Dies ist beim Lösen linearer Systeme hilfreich. Die Algorithmen, die diesen Funktionen zugrunde liegen, werden auch in lsolve verwendet.
1. Geben Sie eine reelle Matrix M ein (sie muss nicht unbedingt quadratisch sein).
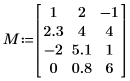
2. Verwenden Sie die Funktion svd, um eine SVD-Zerlegung der Matrix M durchzuführen. Vergrößern Sie die verschachtelten Matrizen, um ihren Inhalt anzuzeigen.

3. Zeigen Sie, dass die Funktion svds einen Vektor singulärer Werte der Matrix M zurückgibt und dass er mit dem ersten verschachtelten Array der Ergebnisse identisch ist, die von der Funktion svd zurückgegeben werden.
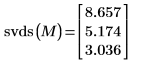
4. Legen Sie die Variablen s, U und V fest, dass sie zu den Elementen 0, 1 und 2 der Matrix S werden.
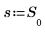
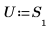
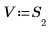
5. Verwenden Sie die Funktion diag, um eine Matrix zu erstellen, deren diagonale Elemente die Elemente von s sind.

6. Zeigen Sie, dass das Produkt von U, D und V die Eingabematrix M zurückgibt.
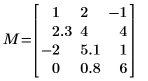
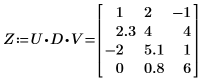
Die beiden Matrizen sind identisch.