Rationale Funktionsregression
• rationalfit(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"])– Übergibt Parameter und deren Vertrauensgrenzen für eine rationale Polynomanpassung der Ordnung m und n oben und unten oder ein zulässiges Residuum-Chi-Quadrat, falls die Funktion die optimale Ordnung bestimmen soll. Das Vertrauensniveau conf wird mit optionalen Standardabweichungen Stdy und optionalen unteren und oberen Grenzen für zulässige Parameterwerte erreicht. Wenn das optionale Zeichenfolgenargument "noscale" angegeben ist, werden die Eingabedaten vor der Berechnung nicht auf den Bereich 0 bis 1 skaliert.
• rationalfitnp(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"]) – Entspricht rationalfit, vermeidet jedoch Pole in der resultierenden rationalen Funktion. Der Standardwert für Acc ist 10-7.
Die rationale Anpassungsfunktion hat folgende Form:
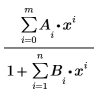
Dabei gilt: mund n sind der gewünschte Grad von Zähler und Nenner.
Die Ausgabe von rationalfit oder von rationalfitnp ist eine Matrix mit drei Spalten, wobei die erste Spalte die Werte für die angepassten Parameter und die zweite und dritte Spalte den linken bzw. rechten Rand für das Konfidenzintervall der Parameter enthält.
Argumente
• vx, vy sind gleich lange Vektoren mit reellen Datenwerten.
• conf ist die gewünschte Vertrauensgrenze, ein als Zahl zwischen 0 und 1 (inklusive) ausgedrückter Prozentwert.
• m, n sind ganzzahlige Polynomordnungen für den Zähler und den Nenner der anzupassenden rationalen Funktion. Die Summe aus m und n darf die Länge von vx nicht überschreiten.
• Stdy (optional) ist ein Vektor von Standardabweichungen in y. Stdy muss die gleiche Länge haben wie vy.
• LBUB (optional) ist eine zweispaltige Matrix unterer und oberer Grenzen der Parameter mit m + n Zeilen.
• Acc (optional) ist eine Konvergenzgenauigkeit. Der Standardwert für Acc ist 10-7.
• "noscale" (optional) ist ein Zeichenfolgenargument. Ist dieses Argument angegeben, werden die Eingabedaten vor der Berechnung nicht auf den Bereich von 0 bis 1 skaliert.
Wenn Sie mehr als eines der optionalen Argumente verwenden, müssen sie in ihrer relativen Reihenfolge, wie in den Funktionsdefinitionen gezeigt, angegeben werden.