Beispiel: Rationale Funktionsregression 1
rationalfit
Verwenden Sie die Funktion rationalfit, um ein rationales Polynom an Daten anzupassen.
1. Definieren Sie einen Datensatz.

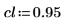
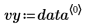
Der Datensatz stammt aus der NIST-Studie zur Elektronenbeweglichkeit von Halbleitern. Die Prädikator-Variable vx ist der natürliche Logarithmus der Dichte. Die Antwortvariable vy ist ein Maß der Elektronenbeweglichkeit.
2. Geben Sie einen Grad für den Zähler und den Nenner der rationalen Funktion an.

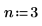
Die Anpassungsfunktion hat folgende Form:
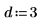
3. Definieren Sie eine Vertrauensgrenze.
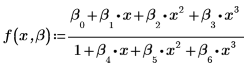
4. Rufen Sie die Funktion rationalfit auf.
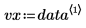
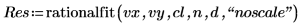
Die erste Spalte der Ausgabe enthält die Werte für die Parameter. Die zweite und dritte Spalte enthalten die Werte für die untere bzw. obere Vertrauensgrenze.
5. Vergleicht die Parameterwerte mit den richtigen Werten, die auf der NIST-Website zu finden sind.


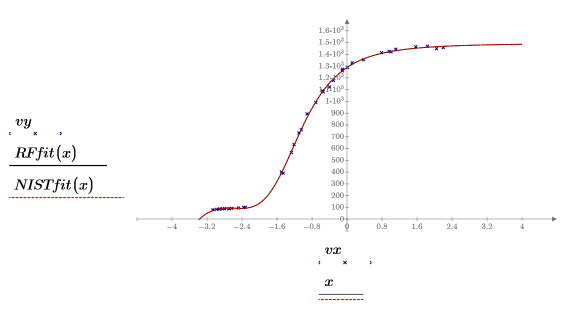
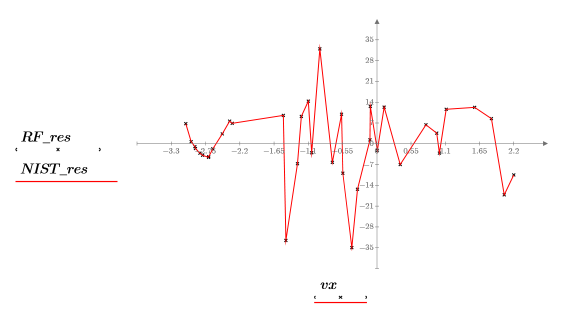
6. Plotten Sie die Daten, die rationale Funktionsregression und die durch die NIST-Parameter definierte Anpassung.

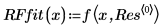
Die Anpassung der rationalen Funktionsregression ist fast perfekt. Dies wird durch den Korrelationskoeffizienten bestätigt.
Residuendiagramm
Erstellen Sie ein Residuendiagramm, um die Güte der Anpassung für die obige Regression grafisch darzustellen.
1. Definieren Sie den Freiheitsgrad.
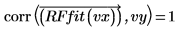
2. Berechnen Sie die Residuen.
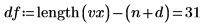
3. Berechnen Sie die Residualquadratsumme.
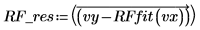
4. Berechnen Sie die Standardabweichung.
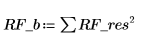
5. Wiederholen Sie die Schritte 2 bis 4 mit den Werten der NIST-Website.
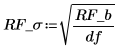
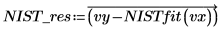
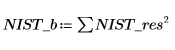
6. Vergleichen Sie die Ergebnisse für die beide Anpassungen.
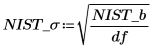
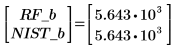
7. Plotten Sie die Datenpunkte und die Residuen.
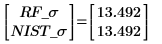
Bedingungen, Standardabweichung und Toleranz
rationalfit hat mehrere optionale Argumente: den Standardabweichungsvektor, die Matrix der unteren und oberen Grenzen, die Genauigkeit und "no scale". Sie können jedes dieser optionalen Argumente für sich allein angeben, bei den ersten drei der oben definierten Argumente ist jedoch die Reihenfolge der Argumente relevant.
1. Erstellen Sie eine Matrix mit unteren und oberen Schranken für die Parameter.
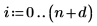
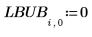
2. Erstellen Sie für die Parameter einen Vektor mit Standardabweichungen.
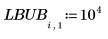
Wenn ein Vektor von Standardabweichungen als Argument der Funktion rationalfit angegeben wird, minimiert der Gleichungslöser die folgende Funktion:
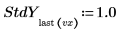
Ist die Standardabweichung für einen Punkt gleich 0, dann wird an diesem Punkt die ursprüngliche, nicht abgeleitete Funktion verwendet, d.h. StdYi wird gleich 1 gesetzt.
3. Legen Sie die Genauigkeit fest. Der Standardwert lautet 10-7.
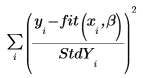
4. 4. Rufen Sie die Funktion rationalfit auf. Vergleichen Sie die zurückgegebenen Parameterwerte mit den korrekten Werten aus der NIST-Website.
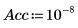
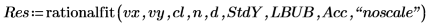
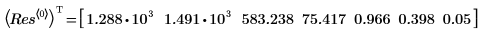
Die Funktion rationalfit führt eine automatische Skalierung der Eingabedaten durch, sodass die Genauigkeit unveränderlich bleibt. Anschließend werden die Ausgabeparameter neu skaliert, sodass sie den ursprünglichen Daten entsprechen. Dadurch lässt sich meistens sicherstellen, dass die Anpassung unabhängig von der relativen Skalierung der Eingabedaten erzielt wird. Wenn es Probleme bereitet, eine gute Anpassung zu erreichen, hängen Sie die Zeichenfolge der Option “noscale” an das Ende der Argumentliste, um diese Option zu deaktivieren.