Nicht-Konvergenz der numerischen Auswertung von Integralen mit unendlichen Grenzwerten
Dieses Thema enthält ein Workaround für zwei Nicht-Konvergenz-Fehler, wenn Integrale mit einem oder zwei unendlichen Integrationsgrenzen ausgewertet werden.
Definieren Sie einen Mittelwert μ und eine Standardabweichung σ, um diese beiden Fälle zu erklären.
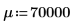
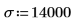
Fall I: Integral mit einer unendlichen Integrationsgrenze
Legen Sie die Multiplikatorvariable n auf 1 fest, und definieren Sie anschließend die Funktion g(x) in Bezug auf die eingebaute Wahrscheinlichkeitsdichte-Funktion dnorm .
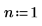
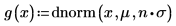
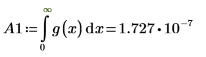
Bei n=1 wird bei der Auswertung des Integrals g(x) über dem Bereich [0, ∞] kein Fehler zurückgegeben, es wird jedoch ein sehr kleiner Wert zurückgegeben.
Workaround für Fall I
Erhöhen Sie den Wert für n auf n=2 und werten Sie das Integral erneut aus.
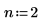
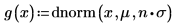
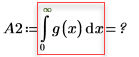
Das Erhöhen des Werts für n auf n=2 führt zu einem Fehler, da die Berechnung nicht zu einer Lösung konvergiert.
Legen Sie, um das Problem zu umgehen, die Variable T auf einen Wert fest, der nahe am Ende von g(x) liegt, und trennen Sie dann das einzelne Integral in zwei Integrale: eines für den Bereich [0, T] und eines für den Bereich [T, ∞].
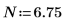 | 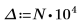 |
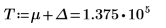 |
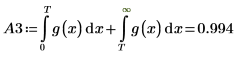
Das aufgeteilte Integral A3 gibt bei n=1 oder n=2 eine gute Antwort zurück. Plotten Sie g(x) und fügen Sie die vertikale Markierung T hinzu, um zu sehen, wie nahe sich diese am Ende von g(x) befindet.
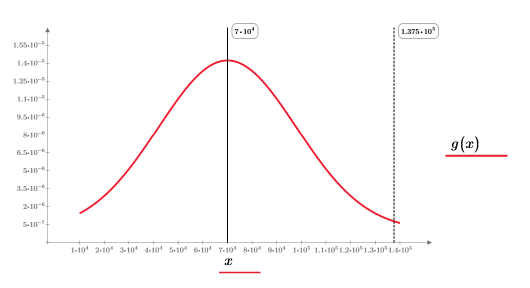
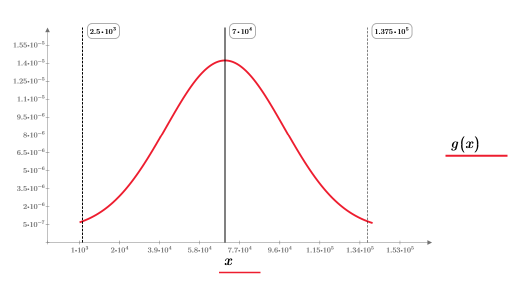
Das Diagramm zeigt die Variable T als vertikale Markierung nahe dem Ende von g(x).
Fall II: Integral mit zwei unendlichen Integrationsgrenzen
Legen Sie die Multiplikatorvariable n auf 1 fest und werten Sie anschließend das Integral g(x) über den Bereich [-∞, ∞] aus.
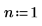
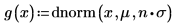
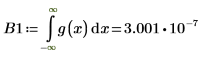
Bei n=1 wird bei der Auswertung des Integrals g(x) über dem Bereich [-∞, ∞] kein Fehler zurückgegeben, es wird jedoch ein sehr kleiner Wert zurückgegeben.
Workaround für Fall II
Legen Sie, um das Problem zu umgehen, die Variablen T1 und T2 auf Werte, die sich nahe am Anfang und Ende von g(x) befinden, fest, und trennen Sie dann das einzelne Integral in drei Integrale: eines für den Bereich [-∞, T1], eines für den Bereich [T1, T2] und eines für den Bereich [T2, ∞].
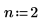
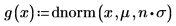
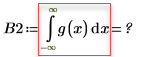
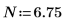 | 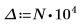 |
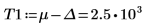 | 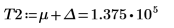 |
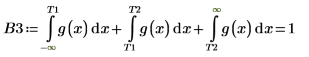
Das aufgeteilte Integral gibt bei n=1 oder n=2 eine gute Antwort zurück. Plotten Sie g(x) und fügen Sie die vertikalen Markierungen T1 und T2 hinzu, um zu sehen, wie nahe sich diese am Anfang und Ende von g(x) befinden.
Beobachtungen und Schlussfolgerungen
Plotten Sie die eingebaute Wahrscheinlichkeitsdichte-Funktion dnorm mit demselben Mittelwert aber zwei unterschiedlichen Werten für die Standardabweichung.
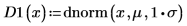
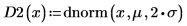
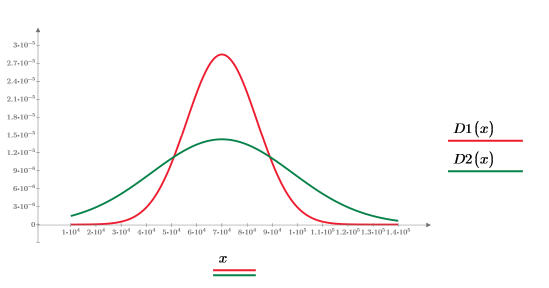
Das Diagramm zeigt Folgendes:
• Der kleinere Standardabweichungs-Wert bewirkt, dass sich der größte Teil der Fläche unter der Kurve näher am Mittelwert befindet. In diesem Fall konvergiert die numerische Berechnung, gibt aber die falsche Antwort zurück.
• Der größere Standardabweichungs-Wert bewirkt, dass sich der größte Teil der Fläche unter der Kurve weiter vom Mittelwert weg befindet. In diesem Fall kann die numerische Berechnung nicht konvergiert werden.
In beiden Fällen wird durch Trennen des Integrals sichergestellt, dass die Berechnung konvergiert und die richtige Antwort zurückgibt.