Multivariate Polynomregression
• polyfit(X, Y, n/"terms"/M) – Definiert eine Funktion, die eine multivariate Polynomregressionsfläche beschreibt, welche die in Matrix Y aufgezeichneten Ergebnisse an die in Matrix X gefundenen Daten anpasst. Die Polynomregressionsgleichung kann durch ihren Polynomgrad n oder durch ihre Ausdrücke definiert werden, die in der Zeichenfolge “terms” oder in der Matrix M angegeben werden. Verwenden Sie Matrix M, wenn der Achsenabschnitt nicht in die Polynomanpassung einbezogen werden soll.
Betrachten Sie z.B. die folgende Polynomregressionsfunktion p:
p := polyfit(X, Y ,1)
p(v) = 1.075
Funktion p nimmt ein Vektorargument v an, das einen Wert einer unabhängigen Variablen von p angibt, entsprechend der Beschreibung in Matrix X. Jede Variable in Vektor v muss Einheiten aufweisen, die mit der entsprechenden Spalte von Matrix X kompatibel sind. Die von der Anpassungsfunktion p zurückgegebenen Einheiten sind kompatibel mit den Einheiten von Matrix Y.
Argumente
• X ist eine Konstruktionsmatrix oder eine Matrix, in der jede Spalte eine unabhängige Variable darstellt. Jede Spalte von X muss kompatible Einheiten enthalten.
• Y ist ein Vektor oder eine Matrix gemessener oder simulierter Ergebnisse, wobei jede Zeile die Ergebnisse für jeden Rechenlauf oder alle in X definierten Datenpunkte enthält. Wenn die Zeilen nicht jeweils die gleiche Anzahl von Replikaten enthalten, müssen Sie die leeren Elemente von Y mit NaNs auffüllen. Die Elemente von Y müssen kompatible Einheiten enthalten.
• n ist eine Ganzzahl, die den Polynomgrad angibt. Sie muss kleiner sein als die Gesamtmenge der Datenpunkte: 1 ≤ n ≤ length(Y) − 1. Andernfalls ist das Problem unterbestimmt und hat keine eindeutige Lösung.
• “terms” ist eine Zeichenfolge, die Ausdrücke oder die Faktoren und Interaktionen angibt, die bei der Polynomregression einbezogen werden sollen. "A B AB AA BB" bedeutet, dass das Polynom die folgenden Ausdrücke enthält:
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
Als Trennzeichen können Sie ein Leerzeichen, ein Komma, einen Doppelpunkt oder ein Semikolon verwenden.
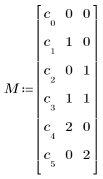
• M ist eine Matrix, die ein Polynom angibt. Die erste Spalte enthält Schätzwerte für die Koeffizienten, die übrigen Spalten enthalten die Potenz der unabhängigen Variablen für jeden Ausdruck. Definieren Sie M für das oben beschriebene Polynom folgendermaßen:
Zusätzliche Informationen
Im Thema Veraltete Funktionen wird die Verwendung der Funktion polyfit als Alternative zur als veraltet markierten Funktion regress empfohlen.
Die Funktion regress gibt eine Matrix von Koeffizienten zurück, die der Funktion interp übergeben wird, um die Anpassungsfunktion zu erhalten.
Die Funktion polyfit gibt eine Anpassungsfunktion zurück, und daher muss die Funktion interp nicht aufgerufen werden.