Beispiel: Die Chirp-z-Transformation

Funktionen > Signalverarbeitung > Spektralanalyse > Beispiel: Die Chirp-z-Transformation

Bei der Chirp-z-Transformation wird das Spektrum eines abgetasteten Signals bei gleichmäßig verteilten Frequenzwerten über ein kleines Frequenzintervall interpoliert.

Der für die Chirp-z-Transformation verwendete Algorithmus wird in Samuel Stearns und Ruth David, Signal Processing Algorithms (Prentice-Hall, Inc.) beschrieben.

Signal erstellen

1. Definieren Sie die Signalfrequenzen.

2. Verwenden Sie die Funktionen exp und sin, um ein abnehmendes Sinuswellensignal zu definieren.

<region id="ID0EMKC3" actualWidth="68.5" actualHeight="25.6" top="307.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="184"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve">K</id> <real>1000</real> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E1KC3" actualWidth="89.976666666666674" actualHeight="25.6" top="307.20000000000005" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="186"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve">k</id> <range> <real>0</real> <apply> <minus /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id> <real>1</real> </apply> </range> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EILC3" actualWidth="71.07" actualHeight="47.2" top="307.20000000000005" left="288.00000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="188"> <define xmlns="http://schemas.mathsoft.com/math50"> <function> <id labels="VARIABLE" xml:space="preserve">f</id> <boundVars> <id labels="VARIABLE" xml:space="preserve">k</id> </boundVars> </function> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">K</id> </apply> </define> </math> </region>
<region id="ID0E3LC3" actualWidth="230.96" actualHeight="36.800000000000004" top="345.6" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="190"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="" xml:space="preserve">x</id> <id labels="" xml:space="preserve">k</id> </apply> <apply> <mult /> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">exp</id> <apply> <mult /> <apply> <neg /> <id xml:space="preserve">k</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f1</id> </apply> </apply> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">sin</id> <apply> <mult /> <apply> <mult /> <apply> <mult /> <real>2</real> <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id> </apply> <id xml:space="preserve">k</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f2</id> </apply> </apply> </apply> </define> <resultFormat> <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" /> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

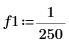
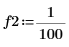
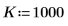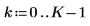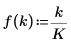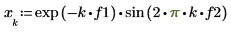Das abnehmende Sinuswellensignal ist das Produkt einer Exponentialfunktion, die mit der Zeit auf null abfällt, und einer Sinuswellenfunktion.

3. Plotten Sie das abnehmende Signal.

<region id="ID0ETNC3" actualWidth="575.054590305129" actualHeight="312" top="460.80000000000007" left="38.400000000000006" height="312" width="575.054590305129" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="192">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="479.054590305129" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="1">
          <axisLine position="origin" positionticmark="4" legendWidth="82.1733333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="193">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="194">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.8" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="66.2233333333333" />
          <axisGrid>
            <gridFrequency>10</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="195">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="196">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

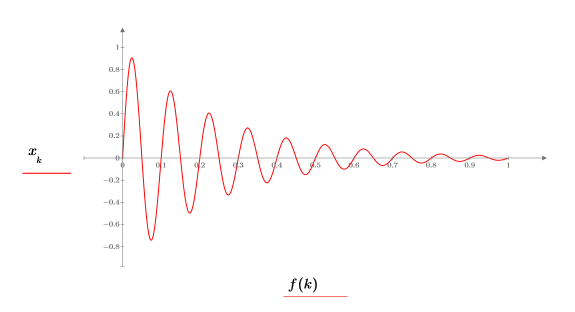
Die Frequenz wird normalisiert, sodass 1 die Abtastfrequenz repräsentiert.

4. Verwenden Sie die Funktion dft, um die DFT des Signals zu berechnen.

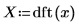
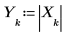
5. Plotten Sie die DFT des Signals. Verwenden Sie vertikale Markierer, um den Betrag und die Frequenz der ersten Spitze anzuzeigen.

<region id="ID0EKSC3" actualWidth="575.50769230769242" actualHeight="312" top="998.40000000000009" left="38.400000000000006" height="312" width="575.50769230769242" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="207">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.307692307692" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="82.1733333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="208" display="true" color="#FF2E3192" line-style="Dash" value="0.01">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">f2</id>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="210">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="211">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="150">
          <axisLine position="origin" positionticmark="0" legendWidth="68.8633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="212" display="true" color="#FF068149" line-style="Dash" value="122.64826285536819">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">m<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">y</Subscript></Span>
              </id>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="220">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="221">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="215">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="217">
              <real xmlns="http://schemas.mathsoft.com/math50">30</real>
            </secondTickValue>
            <endValue resultRef="219">
              <real xmlns="http://schemas.mathsoft.com/math50">150</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

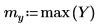
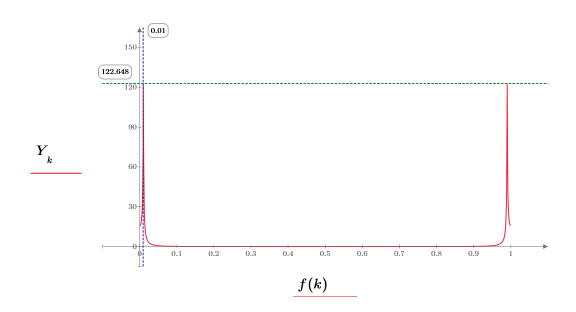
Die Spitze tritt bei der Frequenz der Sinuswelle auf, gefaltet mit dem Spektrum der Exponentialfunktion.

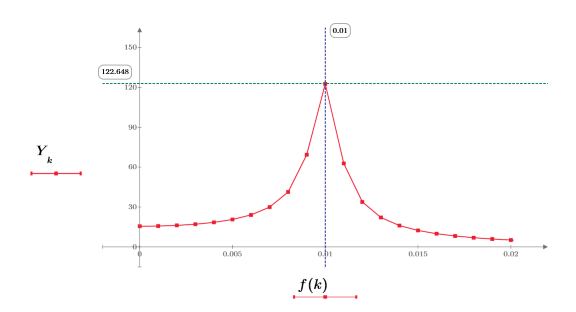
6. Vergrößern Sie die erste Spitze, indem Sie die Frequenzskala entlang der X-Achse erweitern.

<region id="ID0ENWC3" actualWidth="575.73846153846148" actualHeight="311.99999999999994" top="1440.0000000000002" left="38.400000000000006" height="311.99999999999994" width="575.73846153846148" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="237">
          <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.538461538461" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="0.02">
          <axisLine position="origin" positionticmark="0" legendWidth="82.1733333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="238" display="true" color="#FF2E3192" line-style="Dash" value="0.01">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">f2</id>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="246">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="247">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="241">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">lo</id>
            </startValue>
            <secondTickValue resultRef="243">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
            </secondTickValue>
            <endValue resultRef="245">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">hi</id>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="150">
          <axisLine position="origin" positionticmark="0" legendWidth="68.8633333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="248" display="true" color="#FF068149" line-style="Dash" value="122.64826285536819">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">
                <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">m<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">y</Subscript></Span>
              </id>
            </marker>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="256">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="257">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="251">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="253">
              <real xmlns="http://schemas.mathsoft.com/math50">30</real>
            </secondTickValue>
            <endValue resultRef="255">
              <real xmlns="http://schemas.mathsoft.com/math50">150</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

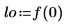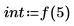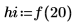7. Berechnen Sie die Anzahl der Datenpunkte innerhalb des Frequenzbereiches.

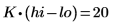
chirpz

Verwenden Sie die Funktion chirpz, um sich das Spektrum um den Spitzenwert genauer anzusehen, indem Sie die Anzahl der Datenpunkte erhöhen.

1. Legen Sie den Schrittparameter fest, und verwenden Sie die Funktion chirpz, um das Spektrum zu berechnen.

<region id="ID0ED2C3" actualWidth="194.00333333333333" actualHeight="25.6" top="2035.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="274">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">S1</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">chirpz</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">lo</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">hi</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">step1</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

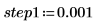
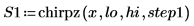
2. Berechnen Sie die Anzahl von Punkten im interpolierten Spektrum.

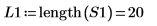
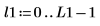
3. Überlagern Sie die erste Spitze der DFT und das interpolierte Spektrum mit dem neuen Bereich.

<region id="ID0EV5C3" actualWidth="575.50769230769242" actualHeight="350.4" top="2208.0000000000005" left="38.400000000000006" height="350.4" width="575.50769230769242" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="280">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="2" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="281">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.307692307692" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="0.02">
          <axisLine position="origin" positionticmark="0" legendWidth="109.913333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="288">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="289">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="290">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">step1</id>
                </apply>
              </math>
              <math resultRef="291">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="283">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">lo</id>
            </startValue>
            <secondTickValue resultRef="285">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
            </secondTickValue>
            <endValue resultRef="287">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">hi</id>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="150">
          <axisLine position="origin" positionticmark="0" legendWidth="86.44" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="298">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="299">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="300">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <indexer />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">S1</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l1</id>
                  </apply>
                </apply>
              </math>
              <math resultRef="301">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="293">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="295">
              <real xmlns="http://schemas.mathsoft.com/math50">30</real>
            </secondTickValue>
            <endValue resultRef="297">
              <real xmlns="http://schemas.mathsoft.com/math50">150</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Ein Schritt von 0.001 führt zur selben Anzahl von Datenpunkten in der Chirp-Z-Spurkurve. Somit scheinen die beiden Spurkurven identisch zu sein.

4. Reduzieren Sie die Schrittgröße 10-fach, und berechnen und plotten Sie die beiden Funktionen neu.

<region id="ID0EXAD3" actualWidth="194.00333333333333" actualHeight="25.6" top="2726.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="318">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">S2</id>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">chirpz</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">lo</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">hi</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">step2</id>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

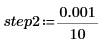
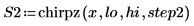
5. Berechnen Sie die neue Anzahl von Punkten im interpolierten Spektrum.

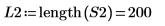
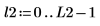
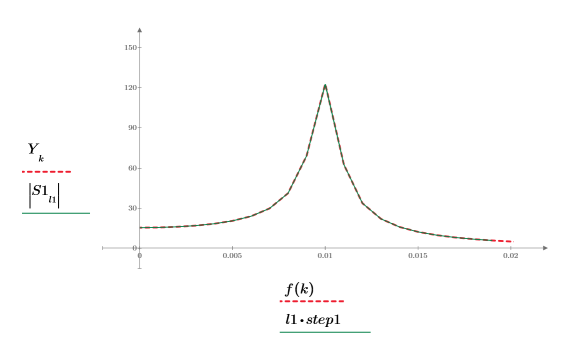
6. Überlagern Sie die erste Spitze der DFT und das neu interpolierte Spektrum.

<region id="ID0EJED3" actualWidth="575.507692307692" actualHeight="350.4" top="2899.2000000000003" left="38.400000000000006" height="350.4" width="575.507692307692" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="324">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="325">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.307692307692" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="0.02">
          <axisLine position="origin" positionticmark="0" legendWidth="109.913333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="332">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">f</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="333">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="334">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l2</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">step2</id>
                </apply>
              </math>
              <math resultRef="335">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="327">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">lo</id>
            </startValue>
            <secondTickValue resultRef="329">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
            </secondTickValue>
            <endValue resultRef="331">
              <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">hi</id>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="150">
          <axisLine position="origin" positionticmark="0" legendWidth="86.44" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="342">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Y</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
                </apply>
              </math>
              <math resultRef="343">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="344">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <indexer />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">S2</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l2</id>
                  </apply>
                </apply>
              </math>
              <math resultRef="345">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="337">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="339">
              <real xmlns="http://schemas.mathsoft.com/math50">30</real>
            </secondTickValue>
            <endValue resultRef="341">
              <real xmlns="http://schemas.mathsoft.com/math50">150</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

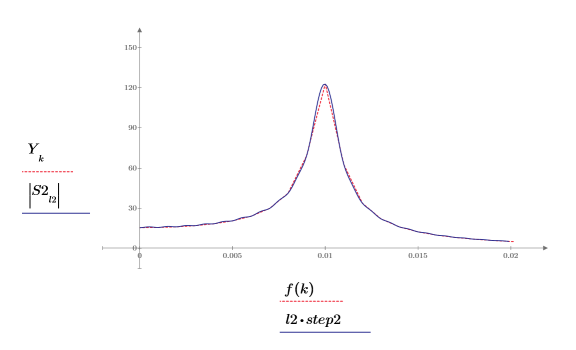
Das Diagramm zeigt, dass mit zunehmender Anzahl der interpolierten Punkte die Spektrumsspurkurve um den Spitzenwert runder wird.

7. Reduzieren Sie step2 erneut 10-fach, und beobachten Sie den Effekt auf das oben dargestellte Diagramm.

Zugehörige Themen

Chirpz-Transformation

War dies hilfreich?