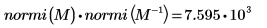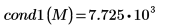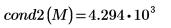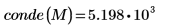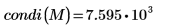Beispiel: Spezielle Eigenschaften von Matrizen

Vektoren, Matrizen und Tabellen > Arbeiten mit Arrays > Beispiel: Spezielle Eigenschaften von Matrizen

Beispiel: Spezielle Eigenschaften von Matrizen

Suchen Sie die Spur, den Rang, das verallgemeinerte Inverse, die Normen und die Konditionszahlen einer quadratischen Matrix.

Die Spurkurve, der Rang und das verallgemeinerte Inverse einer Matrix

1. Verwenden Sie die Funktion tr, um die Spurkurve oder die Summe der diagonalen Elemente von M zu ermitteln.

2. Verwenden Sie die Funktion rank, um den Rang der reellwertigen Matrix M zu ermitteln.

3. Verwenden Sie die Funktion geninv, um das generalisierte Inverse der Matrix M zu ermitteln.

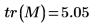
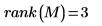
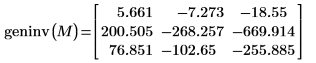
Unterschiedliche Normen einer Matrix

1. Ermitteln Sie die Norm L1 von M, und vergleichen Sie das Ergebnis mit der Ausgabe der Funktion norm1.

Die Norm L1 ist das Maximum der absoluten Spaltensummen (Maximum für j= 0, 1, 2).

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EUFIHB" top="1056.0000000000002" left="19.200000000000003" height="136.00000000000003" width="191.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

2. Verwenden Sie die Funktion norm2, um die Norm L2 von M zu ermitteln.

3. Verwenden Sie die Funktion norme, um die Euklid-Norm von M zu ermitteln:

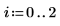
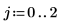
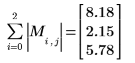
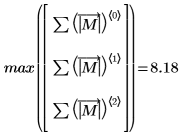
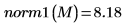
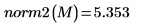
Die Euklid-Norm einer Matrix ist analog der Euklid-Norm eines Vektors:

<region id="ID0EWKIHB" top="1440.0000000000002" left="38.400000000000006" height="60.441333557128914" width="176.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="59">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <pow />
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">i</id>
              </boundVars>
              <apply>
                <summation />
                <lambda>
                  <boundVars>
                    <id xml:space="preserve">j</id>
                  </boundVars>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <indexer />
                        <id xml:space="preserve">M</id>
                        <sequence>
                          <id xml:space="preserve">i</id>
                          <id xml:space="preserve">j</id>
                        </sequence>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </lambda>
                <lowerBound>
                  <real>0</real>
                </lowerBound>
                <upperBound>
                  <real>2</real>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <real>2</real>
            </upperBound>
          </apply>
        </parens>
        <apply>
          <div />
          <real>1</real>
          <real>2</real>
        </apply>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

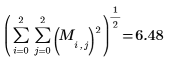
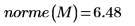
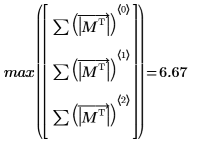
4. Ermitteln Sie die Unendlichnorm von M, und vergleichen Sie das Ergebnis mit der Ausgabe der Funktion normi.

Die Unendlichnorm ist das Maximum der absoluten Zeilensummen (Maximum für i= 0, 1, 2).

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0E3NIHB" top="1766.4000000000003" left="19.200000000000003" height="143.056" width="200.52000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

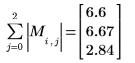
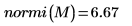
Verschiedene Konditionszahlen einer Matrix

Die Konditionszahl einer Matrix ist das Produkt von zwei Matrixnormen. Sie misst die Sensitivität einer linearen Systemlösung gegenüber Fehlern im Eingabevektor:

1. Verwenden Sie die Funktion cond1, um die Konditionszahl L1 von M zu ermitteln.

2. Verwenden Sie die Funktion cond2, um die Konditionszahl L2 von M zu ermitteln.

3. Verwenden Sie die Funktion conde, um die Euklid-Konditionszahl von M zu ermitteln.

4. Verwenden Sie die Funktion condi, um die Unendlich-Konditionszahl von M zu ermitteln.

Zugehörige Themen

Arbeiten mit Arrays

War dies hilfreich?