Beispiel: Residualanalyse
Berechnen Sie die Residuen eines Datensatzes, um festzustellen, ob die Daten linear verteilt sind. Bevor Sie das Regressionsmodell für Vorhersagen einsetzen, überprüfen Sie, ob die Voraussetzungen für das lineare Modell erfüllt sind:
• Die Fehler müssen unkorreliert sind.
• Für jeden gegebenen Wert von X sollten die Fehler normalverteilt sein, einen Mittelwert von Null und eine konstante Varianz haben.
Normierte Residuen
Zur Interpretation des relativen Betrags der Residuen können Sie diese normieren. Sie müssen die Residuen durch eine Schätzung der Standardfehlerabweichung teilen.
1. Definieren Sie den folgenden Datensatz
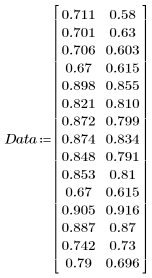
2. Plotten Sie den Datensatz.
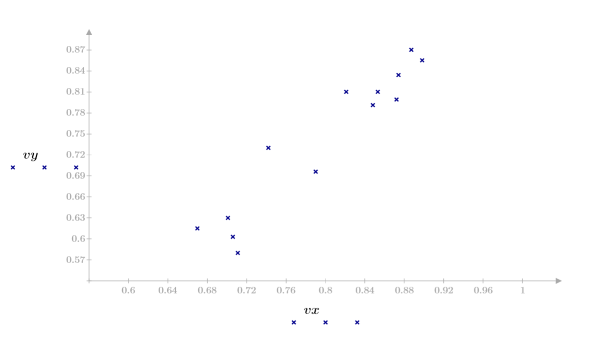
Die Daten scheinen linear zu sein. Dies wird durch den Korrelationskoeffizienten bestätigt, der beinahe 1 ist:
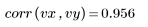
3. Definieren Sie die Mittelwertgerade.
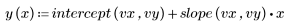
4. Subtrahieren Sie die angepassten Werte von den gemessenen Werten.
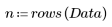
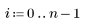
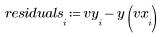
5. Dividieren Sie die Residuen durch den Standardfehler der Schätzung.
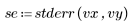
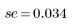
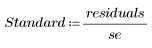
Student-verteilte Residuen
Student-verteilte Residuen bzw. bereinigte normierte Residuen sind eine weitere häufig verwendete Schätzung für den Standardfehler. Bei dieser Schätzung werden die Residuen in Bezug auf den Abstand zwischen den einzelnen Werten von x und den Mittelwert von x bereinigt.
1. Berechnen Sie den Abstand zwischen den Werten und den Mittelwert.
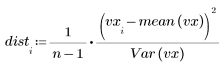
2. Definieren Sie die für jedes Residuum relevante Standardabweichung.

3. Definieren Sie die Student-verteilten Residuen.
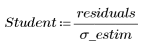
Student-verteilte Residuen sind genauer als normierte Residuen, weil hier die Punkt-zu-Punkt-Differenzen der Fehlervarianz berücksichtigt werden. Die Residuen haben jedoch einen sehr ähnlichen Wert.
 |  |
4. Rufen Sie polyfitstat auf. Zeigen Sie die Teilmatrix der beobachteten Diagnosedaten an, welche die Student-verteilten Residuen enthält.
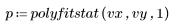
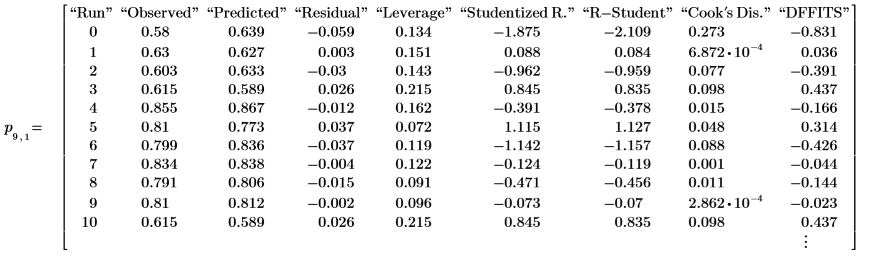
Auf Linearität prüfen
Prüfen Sie, ob zwischen den Daten im Data-Satz eine lineare Beziehung besteht. Erstellen Sie ein Gegenbeispiel mit einer Zufallsstichprobe, deren Daten eine kurvenförmige Beziehung aufweisen. Wenn zwischen den Daten eine lineare Beziehung besteht und die Fehler normalverteilt sind, dann sind in den Streuungsdiagrammen keine Muster erkennbar. Die Punkte sind zufällig um das hypothetische Fehlermittel Null verteilt
1. Plotten Sie die Residuen gegen die x-Werte und gegen die vorhergesagten y-Werte.
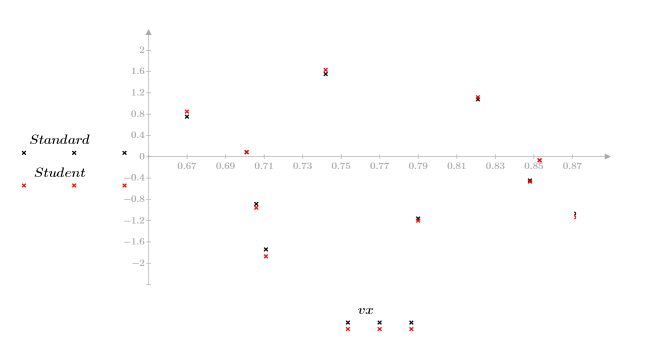
Das Fehlen von Mustern bei den Residuen lässt darauf schließen, dass eine lineare Beziehung zwischen den Daten besteht.
2. Generieren Sie eine Zufallsstichprobe mit Punkten, zwischen denen eine quadratische Beziehung besteht.
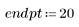
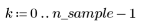
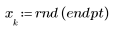
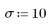
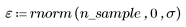
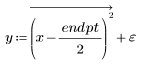
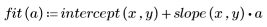
3. Plotten Sie den relativen Betrag der Residuen.
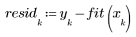
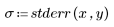
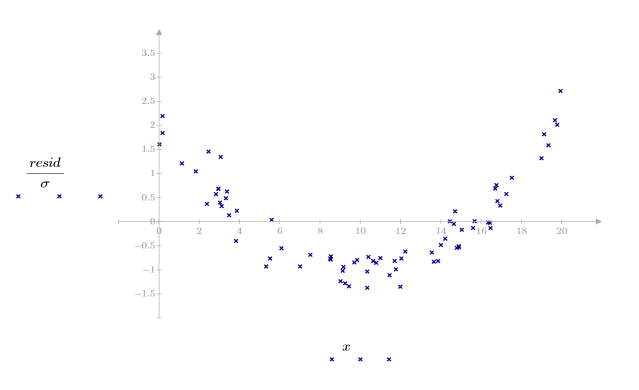
Das Streuungsdiagramm der Residuen spiegelt das quadratische Muster der Daten wider. Zwischen den Daten besteht keine lineare Beziehung.
Auf konstante Fehlervarianzen prüfen
Im Satz Data wurde kein Muster in den Fehlervarianzen erkannt. Erstellen Sie ein Gegenbeispiel, in dem die Daten linear zu sein scheinen, die Fehlervarianzen jedoch nicht normalverteilt sind und in einem Streuungsdiagramm der Residuen entweder eine von links nach rechts zunehmende oder abnehmende Streubreite erkennbar ist.
1. Generieren Sie eine Zufallsstichprobe mit Punkten, die von links nach rechts stärker gestreut werden.
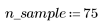
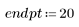
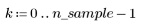
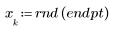
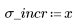
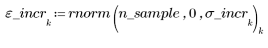
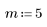
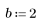
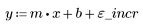
2. Berechnen Sie die Mittelwertgerade. Stellen Sie den zufälligen Datensatz und die Anpassungsfunktion grafisch dar.
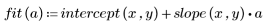
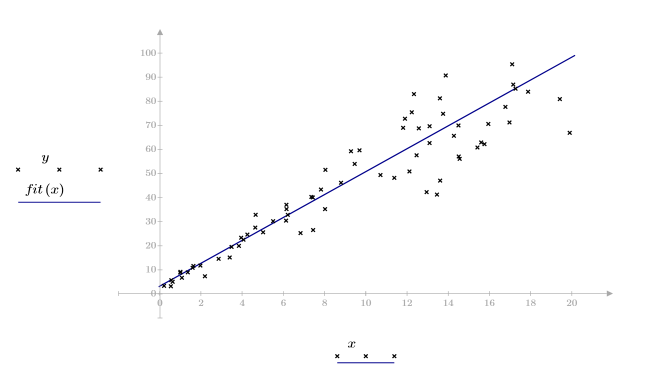
Der Korrelationskoeffizient ist beinahe 1, was auf eine lineare Beziehung zwischen den Daten schließen lässt.
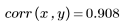
3. Plotten Sie den relativen Betrag der Residuen.
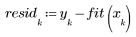
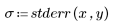
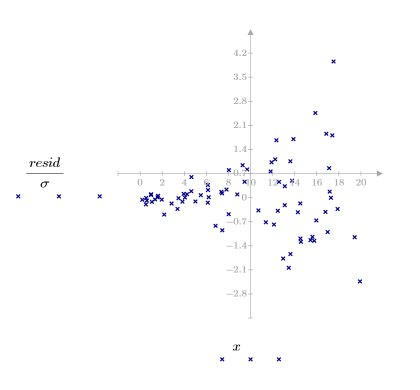
Das Streuungsdiagramm der Residuen scheint nicht zufällig verteilt zu sein. Die Punkte im Streuungsdiagramm der Residuen sind von links nach rechts zunehmend stärker gestreut.
Auf Korrelationsfehler prüfen
Sie können mithilfe der Durbin-Watson-Statistik prüfen, ob aufeinanderfolgende Fehlerausdrücke im linearen Regressionsmodell korreliert sind.
Berechnen Sie die Durbin-Watson-Statistik für den Satz Data:
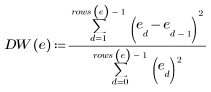
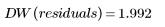
Die Werte der Durbin-Watson-Statistik liegen im Bereich zwischen 0 und 4. Wenn zwei aufeinanderfolgende Ausdrücke unkorreliert sind, dann ist der Durbin-Watson-Wert annähernd 2. Drbin-Watson-Werte kleiner 2 weisen auf positive Korrelationen zwischen aufeinanderfolgenden Werten hin und Werte größer 2 auf negative Korrelationen.
Die Durbin-Watson-Statistik wird in der Berechnung von Kleinste-Quadrate-B-Splines verwendet. Leider können Korrelationen höheren Grades (nicht aufeinander folgender Werte) nicht mithilfe der Durbin-Watson-Statistik erkannt werden. Diese Arten der Korrelation treten selten auf, ohne dass eine Korrelation zwischen zwei aufeinanderfolgenden Werten vorliegt.
Die Durbin-Watson-Statistik ist eine der Statistiken, die von polyfitstat zurückgegeben werden.
Auf Normalität prüfen
Prüfen Sie, ob der Satz Data normalverteilt ist, indem Sie einen Normalplot der normierten Residuen erstellen.
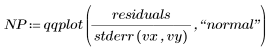
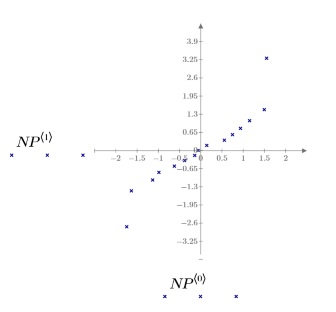
Der Normalplot ähnelt einer Geraden. Die Fehler sind daher näherungsweise normalverteilt. Da die Normalplots auch andere Verstöße gegen die Annahmen darstellen, beispielsweise wenn die Fehlervarianzen nicht gleich sind, empfiehlt es sich, die Prüfung auf Normalität zuletzt durchzuführen.