Beispiel: Die inverse Transformation idft
Die Funktion idft ist die inverse Transformation von dft, sodass erwartet wird, dass diese Funktion die ursprüngliche Dateneingabe für die komplexe Transformation wiederherstellt.
Mit Vektoren (1D) arbeiten
1. Legen Sie die Länge des Vektors v fest.
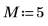
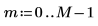
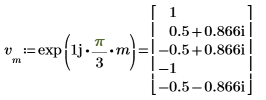
3. Verwenden Sie die Funktion dft zur Berechnung der Vorwärtstransformation des Vektors v.
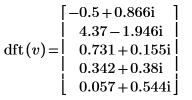
4. Verwenden Sie die Funktion idft zur Berechnung der inversen Transformation des Vektors v.

5. Zeigen Sie, dass die inverse Transformation der Vorwärtstransformation des Vektors v dem ursprünglichen Vektor v .
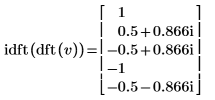 |  |
Die Ergebnisse sind identisch.
Mit (2D) Matrizen arbeiten
1. Definieren Sie die Matrix C, und werten Sie sie aus.
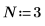
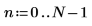
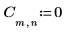
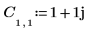
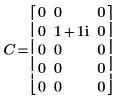
2. Verwenden Sie die Funktion dft zur Berechnung der Transformation der Matrix C.

3. Verwenden Sie die Funktion idft zur Berechnung der inversen Transformation der Matrix C.

4. Zeigen Sie, dass die inverse Transformation der Vorwärtstransformation der Matrix C der ursprünglichen Matrix C entspricht.
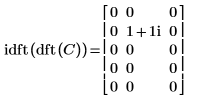 | 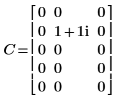 |
Die Ergebnisse sind identisch.
Die idft zugrunde liegende Summe demonstrieren
Eindimensionaler Fall:
1. Verwenden Sie die Funktion exp und den Summenoperator, um die inverse Transformation des Vektors v zu berechnen.
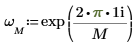
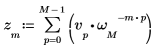
2. Vergleichen Sie sich die resultierende Vorwärtstransformation des Vektors v mit der Ausgabe der Funktion dft.
 | 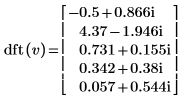 |
Die Ergebnisse sind identisch.
3. Verwenden Sie den Summenoperator zur Berechnung der inversen Transformation des Vektors v.
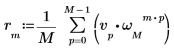
4. Vergleichen Sie sich die resultierende inverse Transformation des Vektors v mit der Ausgabe der Funktion idft.
 |  |
Die Ergebnisse sind identisch.
Zweidimensionaler Fall:
1. Verwenden Sie die Funktion exp und den Summenoperator, um die Vorwärtstransformation der Matrix C zu berechnen.
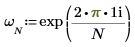
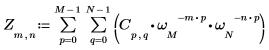
2. Vergleichen Sie sich die resultierende Vorwärtstransformation der Matrix C mit der Ausgabe der Funktion dft.


Die Ergebnisse sind identisch.
3. Verwenden Sie den Summenoperator zur Berechnung der inversen Transformation der Matrix C.
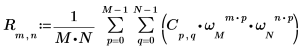
4. Vergleichen Sie sich die resultierende inverse Transformation der Matrix C mit der Ausgabe der Funktion idft.


Die Ergebnisse sind identisch.