Beispiel: Einführung in FFTs
Die schnelle Fourier-Transformation (FFT, Fast Fourier Transformation) stellt eine numerische Methode zum Ausdrücken des zeitlich gemessenen Frequenzinhalts eines Datensatzes dar. Die Daten sind häufig kontinuierlich und bilden eine Wellenform. Um numerisch mit den Daten zu arbeiten, werden sie in regelmäßigen Abständen mit verschiedenen Abtastfrequenzen abgetastet. Die Abbildungen unten zeigen einige abgetastete Wellenformen und die Beträge von deren Fourier-Transformationen, die bezogen auf die Frequenz grafisch dargestellt sind.
Abgetastete Sinuswellenform
1. Verwenden Sie die Funktion sin, um eine sinusförmige Wellenform festzulegen.
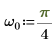
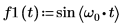
2. Legen Sie die Anzahl der Datenpunkte fest.
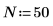
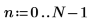
3. Legen Sie den Abstand zwischen den Stichproben fest.
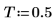
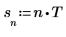
4. Legen Sie die Abtastfrequenz fest.
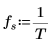
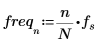
5. Plotten Sie die sinusförmige Funktion.
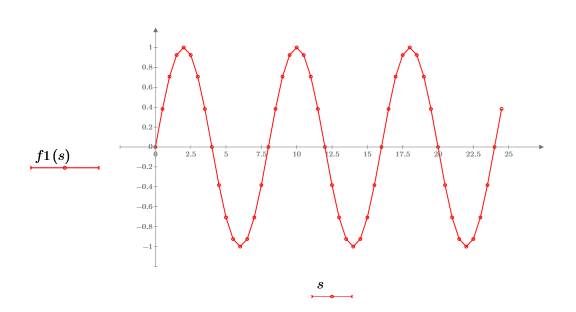
6. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation zu berechnen.
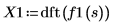
X1 ist ein Vektor reeller oder komplexer Zahlen.
7. Ermitteln Sie die Frequenzen mit den maximalen Beträgen.
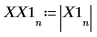
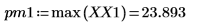
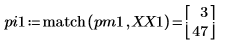
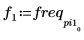
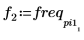
8. Plotten Sie das transformierte Signal, und verwenden Sie Markierungen, um die Frequenz und den Betrag der Spitzenwerte anzuzeigen.
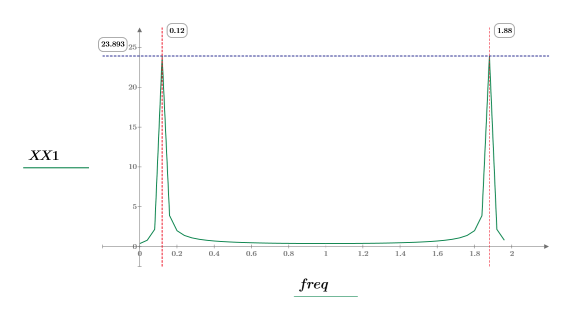
Abgetastete Kosinuswellenform
1. Verwenden Sie die Funktion cos, um eine kosinusförmige Wellenform festzulegen.
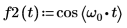
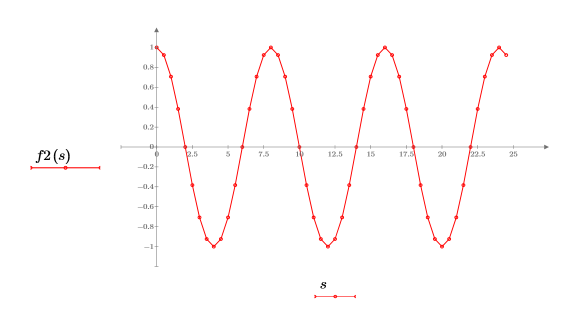
2. Plotten Sie die Kosinusfunktion.
3. Verwenden Sie die Funktion dft, um die diskreten Fourier-Transformationen zu berechnen.
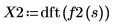
X2 ist ein Vektor reeller oder komplexer Zahlen.
4. Ermitteln Sie die Frequenzen mit den maximalen Beträgen.
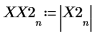
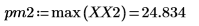
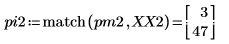
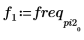
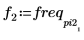
5. Plotten Sie das transformierte Signal, und verwenden Sie Markierungen, um die Frequenz und den Betrag der Spitzenwerte anzuzeigen.
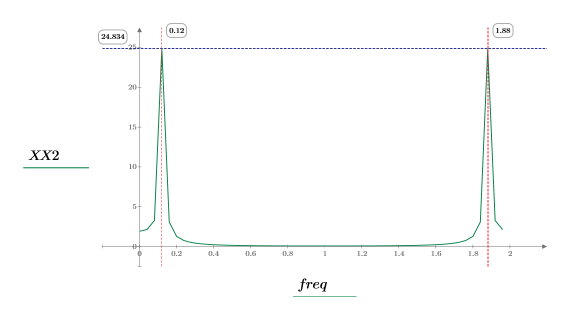
Abgetastete exponentielle Wellenform
1. Verwenden Sie die Funktion exp, um eine exponentielle Wellenform festzulegen.
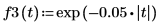
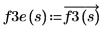
Mit dem Vektorisierungsoperator werden die elementweisen Werte der Funktion abgerufen, weil der Determinantenoperator innerhalb der Definition einen einzelnen Skalarwert zurückgibt.
2. Plotten Sie die exponentielle Funktion.
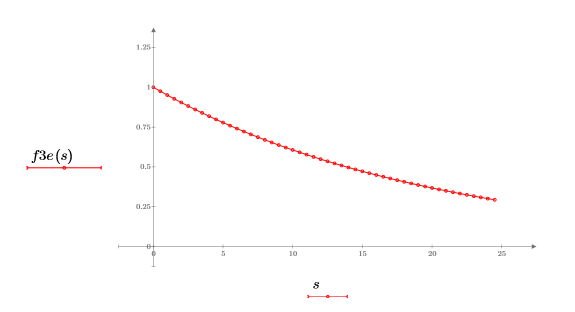
3. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation zu berechnen.
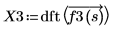
X3 ist ein Vektor reeller oder komplexer Zahlen.
4. Ermitteln Sie die Frequenzen mit den maximalen Beträgen.
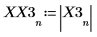
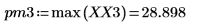
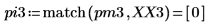
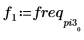
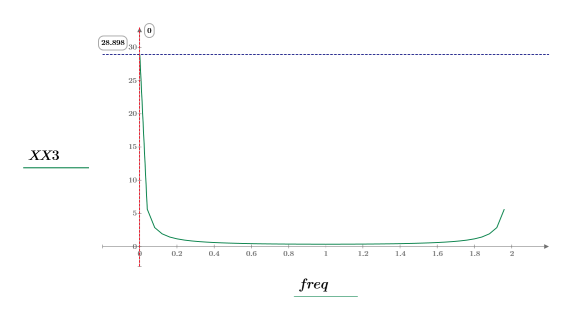
5. Plotten Sie das transformierte Signal, und verwenden Sie Markierungen, um die Frequenz und den Betrag der Spitzenwerte anzuzeigen.
Abgetastete Step-Wellenform
1. Verwenden Sie die Funktion if, um eine stufenförmige Wellenform festzulegen.
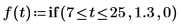
2. Berechnen Sie den Impulsbetrag für jedes Intervall.
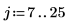
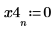
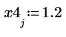
3. Plotten Sie die Schrittfunktion.
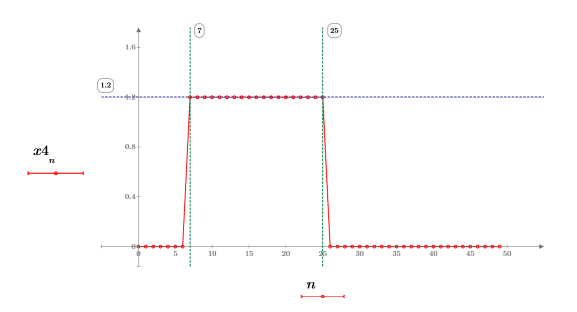
Der Betrag ist gleichmäßig und zwischen 7 und 25 gleich 1.2.
4. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation zu berechnen.
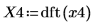
X4 ist ein Vektor reeller oder komplexer Zahlen.
5. Ermitteln Sie die Frequenzen mit den maximalen Beträgen.
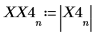
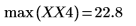
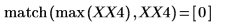
6. Plotten Sie das transformierte Signal, und verwenden Sie Markierungen, um die Frequenz und den Betrag der Spitzenwerte anzuzeigen.
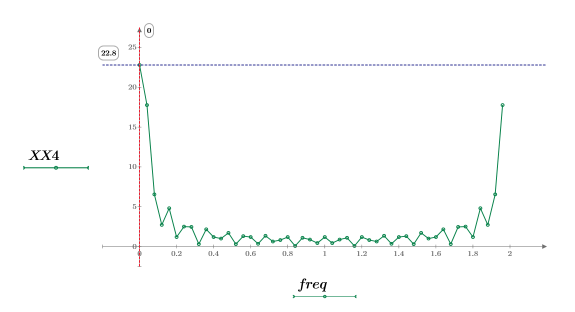
Der maximale Betrag tritt bei freq0 auf.