Beispiel: Vorwärtstransformation dft
Verwenden Sie die Funktion dft, um die komplexe Fourier-Transformation eines reell- oder komplexwertigen Vektors oder einer Matrix mit beliebiger Größe zu ermitteln, und zwar mit einer konstanten Zeit oder einem konstanten Abstand zwischen den Stichproben.
Komplexe 1D-Sinusdaten
Erstellen Sie einen simulierten komplexen Datensatz mit N Datenpunkten und dem Probenabstand T.
1. Definieren Sie die Anzahl der Datenpunkte.
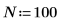
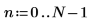
2. Definieren Sie die Zeit T, zu der Stichproben genommen werden.
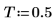
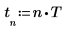
3. Legen Sie die Winkelfrequenz fest.
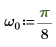
4. Verwenden Sie die Funktion exp, um eine Exponentialfunktion zu definieren.
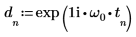
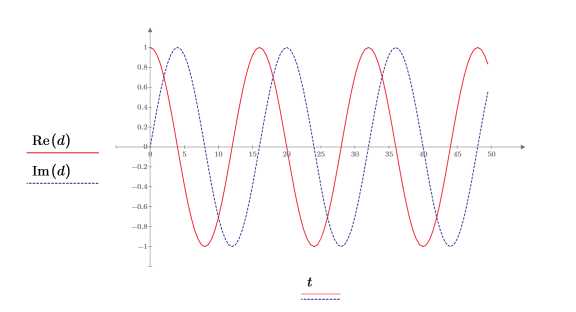
5. Verwenden Sie die Funktionen Re und Im, um die reellen und imaginären Komponenten als Funktionen der Zeit zu extrahieren und zu plotten.
6. Wenden Sie die Funktion dft an, um die Daten in den Frequenzbereich zu transformieren.
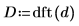
7. Sammeln Sie die absoluten Werte von D in einem neuen Array.
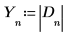
8. Definieren Sie die Abtastfrequenz und die Frequenz, die dem n-ten Eintrag im transformierten Vektor entspricht.
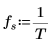
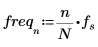
9. Verwenden Sie die Funktionen match und max, um den Spitzenwert und die entsprechende Frequenz innerhalb des transformierten Signals zu suchen.
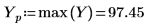
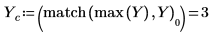
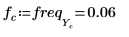
10. Plotten Sie den transformierten Vektor, und verwenden Sie vertikale und horizontale Markierungen, um die Frequenz zu markieren, bei der die Amplitude ihr Maximum erreicht.
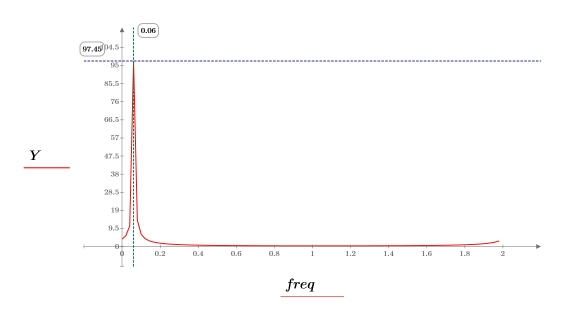
◦ Die obere Hälfte der Frequenzbereichsproben stellen die negativen Frequenzen dar.
◦ Dieses komplexe Signal verfügt über keine negativen Frequenzinhalte.
Zusätzliche Informationen
• Für den reellen Datenvektor v ist der Vektor dft(v) im Allgemeinen komplex und konjugiert symmetrisch zum Mittelwert. Im Fall einer zweidimensionalen reellen Matrix ist jede Spalte des Ergebnisses konjugiert symmetrisch.
• Für jede quadratische Array-Eingabe A ist dft(A) symmetrisch.
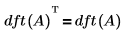
• Gemäß dem Nyquist-Abtasttheorem muss die Abtastfrequenz mindestens das Doppelte der höchsten Frequenz aufweisen, die Sie von der Fourier-Transformation aufgelöst haben möchten.
• Der Primzahlzerleger-Algorithmus, der für die schnelle Fourier-Transformation verwendet wird, verlangsamt sich, wenn es sich bei der Anzahl an Datenpunkten um eine große Primzahl handelt. Dieses Problem tritt möglicherweise niemals auf. Sie sollten es jedoch im Hinterkopf behalten, wenn Sie mit einer großen Primzahl an Datenpunkten arbeiten müssen.