Beispiel: Elementare Zeilenoperationen in Matrizen

Vektoren, Matrizen und Tabellen > Erstellen von Arrays und Tabellen > Beispiel: Elementare Zeilenoperationen in Matrizen

Beispiel: Elementare Zeilenoperationen in Matrizen

Führen Sie drei Arten elementarer Zeilenoperationen an einer m x n-Matrix aus, und zeigen Sie, dass es eine Verbindung mit der Treppennormalform gibt.

1. Definieren Sie eine Eingabematrix:

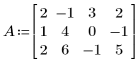
2. Multiplizieren Sie Zeile r mit einem Skalar c:

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EKP5GB" top="144" left="24" width="217.526666666667" height="85.656" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="Variable">e1</id>
        <boundVars>
          <id label="Variable">A</id>
          <id label="Variable">c</id>
          <id label="Variable">r</id>
        </boundVars>
      </function>
      <program>
        <localDefine>
          <id label="Variable">B</id>
          <apply>
            <transpose />
            <id>A</id>
          </apply>
        </localDefine>
        <localDefine>
          <apply>
            <matcol />
            <id label="Variable">B</id>
            <id label="Variable">r</id>
          </apply>
          <apply>
            <mult />
            <id>c</id>
            <apply>
              <matcol />
              <parens>
                <apply>
                  <transpose />
                  <id>A</id>
                </apply>
              </parens>
              <id>r</id>
            </apply>
          </apply>
        </localDefine>
        <apply>
          <transpose />
          <id>B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

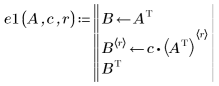
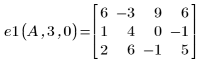
3. Ersetzen Sie Zeile r durch Zeile r plus c-Mal Zeile s:

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EYR5GB" top="360" left="24" width="291.823333333333" height="85.656" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="Variable">e2</id>
        <boundVars>
          <id label="Variable">A</id>
          <id label="Variable">c</id>
          <id label="Variable">r</id>
          <id label="Variable">s</id>
        </boundVars>
      </function>
      <program>
        <localDefine>
          <id label="Variable">B</id>
          <apply>
            <transpose />
            <id>A</id>
          </apply>
        </localDefine>
        <localDefine>
          <apply>
            <matcol />
            <id label="Variable">B</id>
            <id label="Variable">r</id>
          </apply>
          <apply>
            <plus />
            <apply>
              <matcol />
              <parens>
                <apply>
                  <transpose />
                  <id>A</id>
                </apply>
              </parens>
              <id>r</id>
            </apply>
            <apply>
              <mult />
              <id>c</id>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <transpose />
                    <id>A</id>
                  </apply>
                </parens>
                <id>s</id>
              </apply>
            </apply>
          </apply>
        </localDefine>
        <apply>
          <transpose />
          <id>B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

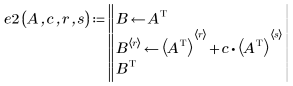
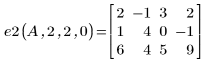
4. Tauschen Sie die Zeilen r und s aus:

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0E5T5GB" top="552" left="24" width="200.72" height="114.808" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="Variable">e3</id>
        <boundVars>
          <id label="Variable">A</id>
          <id label="Variable">r</id>
          <id label="Variable">s</id>
        </boundVars>
      </function>
      <program>
        <localDefine>
          <id label="Variable">B</id>
          <apply>
            <transpose />
            <id>A</id>
          </apply>
        </localDefine>
        <localDefine>
          <apply>
            <matcol />
            <id label="Variable">B</id>
            <id label="Variable">s</id>
          </apply>
          <apply>
            <matcol />
            <parens>
              <apply>
                <transpose />
                <id>A</id>
              </apply>
            </parens>
            <id>r</id>
          </apply>
        </localDefine>
        <localDefine>
          <apply>
            <matcol />
            <id label="Variable">B</id>
            <id label="Variable">r</id>
          </apply>
          <apply>
            <matcol />
            <parens>
              <apply>
                <transpose />
                <id>A</id>
              </apply>
            </parens>
            <id>s</id>
          </apply>
        </localDefine>
        <apply>
          <transpose />
          <id>B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

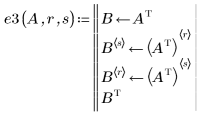
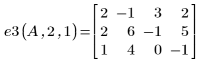
Die Treppennormalform (rref) einer Matrix

Die Treppennormalform ist ein wichtiges Verfahren für die Lösung eines Systems linearer Gleichungen.

Ermitteln Sie mit der folgenden Sequenz der Operationen e1, e2 und e3 die Treppennormalform (rref) von Matrix A:

1. Definieren Sie die Matrix A.

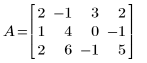
2. Verwenden Sie e2, um Zeile 0 von A durch Zeile 0 plus (-2)-Mal Zeile 1 zu ersetzen:

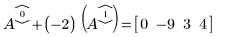
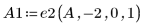
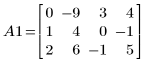
3. Verwenden Sie e2, um Zeile 2 von A1 durch Zeile 2 plus (-2)-Mal Zeile 1 zu ersetzen:

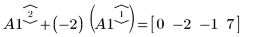
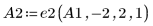
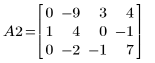
4. Verwenden Sie e1, um Zeile 2 von A2 mit (-1/2) zu multiplizieren:

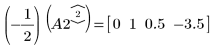
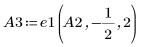
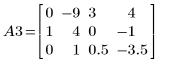
5. Verwenden Sie e2, um Zeile 1 von A3 durch Zeile 1 plus (-4)-Mal Zeile 2 zu ersetzen:

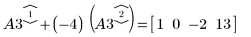
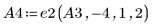
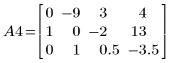
6. Verwenden Sie e2, um Zeile 0 von A4 durch Zeile 0 plus (9)-Mal Zeile 2 zu ersetzen:

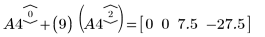
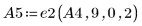
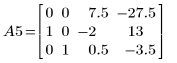
7. Verwenden Sie e1, um Zeile 0 von A5 mit 2/15 zu multiplizieren:

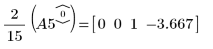
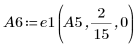
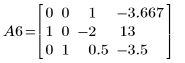
8. Verwenden Sie e2, um Zeile 1 von A6 durch Zeile 1 plus (2)-Mal Zeile 0 zu ersetzen:

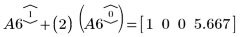
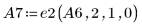
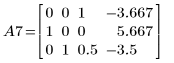
9. Verwenden Sie e2, um Zeile 2 von A7 durch Zeile 2 plus (-1/2)-Mal Zeile 0 zu ersetzen:

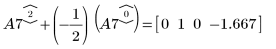
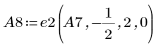
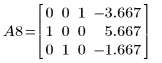
10. Verwenden Sie e3, um die Zeilen 0 und 1 von A8 gegeneinander auszutauschen:

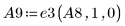
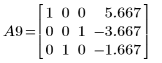
11. Verwenden Sie e3, um die Zeilen 1 und 2 von A9 gegeneinander auszutauschen:

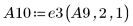
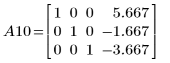
In diesem Beispiel ergibt die obige Sequenz elementarer Zeilenoperationen die Treppennormalform von Matrix A.

12. Verwenden Sie die Funktion rref, um die Treppennormalform von Matrix A zu finden.

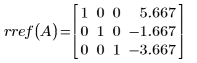
Die zurückgegebene Matrix ist mit Matrix A10 identisch.

Zugehörige Themen

Erstellen von Arrays und Tabellen

War dies hilfreich?