Beispiel: Konfidenzintervall für den Mittelwert

Funktionen > Statistik > Beschreibende Statistik > Beispiel: Konfidenzintervall für den Mittelwert

Berechnen Sie ein Konfidenzintervall für eine Schätzung des Mittelwertes einer normalen Grundgesamtheit, wenn die Varianz der Grundgesamtheit nicht bekannt ist.

1. Definieren Sie einen Stichproben-Datensatz.

2. Verwenden Sie die Funktionen length, mean und stdev, um die Stichprobenstatistiken zu sammeln.

Anzahl der Stichproben	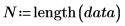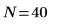<region id="ID0E3MQAB" top="921.60000000000014" left="288.00000000000006" height="25.6" width="125.05666666666667" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="87"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve">N</id> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">length</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">data</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EQNQAB" top="921.60000000000014" left="499.20000000000005" height="25.6" width="60.573333333333338" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="89"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Mittelwert der Stichprobe	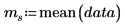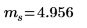<region id="ID0ETOQAB" top="960.00000000000011" left="288.00000000000006" height="27.791200000000003" width="125.12333333333334" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="91"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">m<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">s</Subscript></Span> </id> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">mean</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">data</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EHPQAB" top="960.00000000000011" left="499.20000000000005" height="27.791200000000003" width="86.673333333333346" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="93"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true"> <Span xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation">m<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">s</Subscript></Span> </id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Standardabweichung der Stichprobe	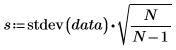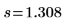<region id="ID0EKQQAB" top="1017.6000000000001" left="288.00000000000006" height="50.065333527326587" width="176.1426666369041" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="95"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve">s</id> <apply> <mult /> <apply> <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">stdev</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">data</id> </apply> <apply> <nthRoot /> <placeholder /> <apply> <div /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id> <apply> <minus /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id> <real>1</real> </apply> </apply> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E5QQAB" top="1017.6000000000001" left="499.20000000000005" height="25.6" width="74.916666666666671" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="97"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">s</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Freiheitsgrade	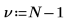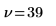<region id="ID0EBSQAB" top="1075.2000000000003" left="288.00000000000006" height="25.6" width="68.183333333333337" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="99"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="*" xml:space="preserve">ν</id> <apply> <minus /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EVSQAB" top="1075.2000000000003" left="499.20000000000005" height="25.6" width="56.493333333333339" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="101"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ν</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

3. Geben Sie das zweiseitige Signifikanzniveau ein.

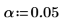
Dies entspricht einem Konfidenzintervall von 95 %.

4. Verwenden Sie die Funktion qt, um das 95. Perzentil der Student-t-Verteilung für einen zweiseitigen Test zu berechnen.

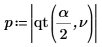
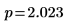
5. Berechnen Sie den oberen und unteren Grenzwert des Konfidenzintervalls.

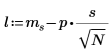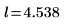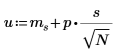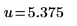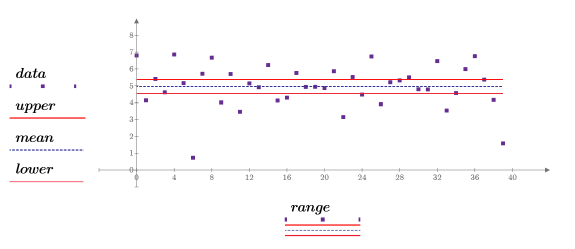
6. Plotten Sie die Beispieldaten, ihren Mittelwert und das Konfidenzintervall.

<region id="ID0EK6QAB" top="1747.2000000000003" left="38.400000000000006" height="249" width="575" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="127">
          <traceStyle color="#FF662D91" symbol="filledRectangle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="128">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="129">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="130">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="455.8" height="172.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="40">
          <axisLine position="origin" positionticmark="0" legendWidth="92.1466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="135">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="136">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="132">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="134">
              <real xmlns="http://schemas.mathsoft.com/math50">40</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="8">
          <axisLine position="origin" positionticmark="0" legendWidth="92.5666666666667" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="143">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">data</id>
              </math>
              <math resultRef="144">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="145">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">upper</id>
              </math>
              <math resultRef="146">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="147">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">mean</id>
              </math>
              <math resultRef="148">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="149">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">lower</id>
              </math>
              <math resultRef="150">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="138">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="140">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="142">
              <real xmlns="http://schemas.mathsoft.com/math50">8</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

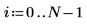
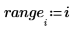
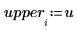
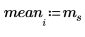
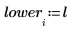
7. Verwenden Sie die Funktion pt, um die kumulative Wahrscheinlichkeitsverteilung für das Konfidenzintervall zu berechnen:

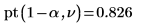
8. Verwenden Sie die Funktion rt, um einen Vektor von Zufallszahlen zu erstellen, die eine Student-t-Verteilung aufweisen:

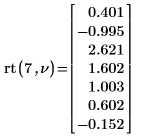
Das Neuberechnen des Arbeitsblatts bewirkt, dass die Funktion rt einen anderen Satz von Zufallszahlen zurückgibt.

Zugehörige Themen

Mittelwertfunktionen

Student-t-Verteilung

War dies hilfreich?