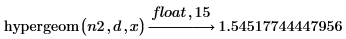Beispiel: Symbolische Funktionen Hypergeom, Mhyper und Fhyper vergleichen

Funktionen > Symbolische Funktionen > Beispiel: Symbolische Funktionen Hypergeom, Mhyper und Fhyper vergleichen

Die Funktion hypergeom

1. Das folgende Integral ist wie folgt mit der hypergeom-Funktion definiert

<region id="ID0EJUVCB" actualWidth="333.12666666666667" actualHeight="80.552" top="76.800000000000011" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="25">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <equal />
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <plus />
              <real>1</real>
              <apply>
                <pow />
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
                <id xml:space="preserve">n</id>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <apply>
        <mult />
        <id xml:space="preserve" labels="FUNCTION">x</id>
        <apply>
          <id xml:space="preserve" labels="FUNCTION">hypergeom</id>
          <sequence>
            <matrix rows="2" cols="1">
              <apply>
                <div />
                <real>1</real>
                <id xml:space="preserve">n</id>
              </apply>
              <real>1</real>
            </matrix>
            <matrix rows="1" cols="1">
              <apply>
                <div />
                <apply>
                  <plus />
                  <id xml:space="preserve">n</id>
                  <real>1</real>
                </apply>
                <id xml:space="preserve">n</id>
              </apply>
            </matrix>
            <apply>
              <neg />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <id xml:space="preserve">n</id>
              </apply>
            </apply>
          </sequence>
        </apply>
      </apply>
    </apply>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

2. Werten Sie das Ergebnis an den Endpunkten des Intervalls [1, 2] aus.

<region id="ID0E1YVCB" actualWidth="682.74000000000012" actualHeight="65.800000000000011" top="211.20000000000005" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="29">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <minus />
        <apply>
          <mult />
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">hypergeom</id>
            <sequence>
              <matrix rows="2" cols="1">
                <apply>
                  <div />
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
                <real>1</real>
              </matrix>
              <matrix rows="1" cols="1">
                <apply>
                  <div />
                  <apply>
                    <plus />
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                    <real>1</real>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </matrix>
              <apply>
                <neg />
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </apply>
            </sequence>
          </apply>
        </apply>
        <apply>
          <mult />
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">hypergeom</id>
            <sequence>
              <matrix rows="2" cols="1">
                <apply>
                  <div />
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
                <real>1</real>
              </matrix>
              <matrix rows="1" cols="1">
                <apply>
                  <div />
                  <apply>
                    <plus />
                    <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                    <real>1</real>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </matrix>
              <apply>
                <neg />
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </apply>
            </sequence>
          </apply>
        </apply>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">float</id>
          <real>14</real>
        </sequence>
      </command>
      <symResult>
        <real>0.10040640511009</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

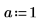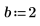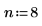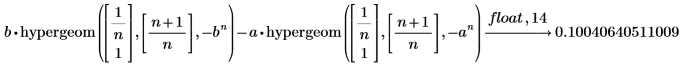
3. Stellen Sie sicher, dass das obige numerische Ergebnis mit dem Wert des folgenden äquivalenten bestimmten Integrals übereinstimmt.

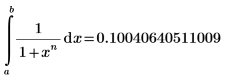
mhyper-Funktion

1. Weisen Sie den Parametern der mhyper-Funktion Werte zu.

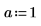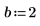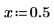2. Werten Sie die Funktion an mhyper(a,b,x) aus.

<region id="ID0ESAWCB" actualWidth="263.32333333333332" actualHeight="25.6" top="460.80000000000007" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="38">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">mhyper</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="15" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

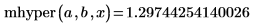
3. Stellen Sie sicher, dass die Funktion hypergeom dieselben Ergebnisse wie mhyper für den Spezialfall zurückgibt, für den gilt:

<region id="ID0EEGWCB" actualWidth="346.40333333333336" actualHeight="39.2" top="518.40000000000009" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="39">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">hypergeom</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
        </sequence>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">float</id>
          <real>15</real>
        </sequence>
      </command>
      <symResult>
        <real>1.29744254140026</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

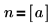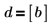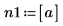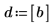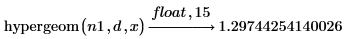
fhyper-Funktion

1. Weisen Sie den Parametern der fhyper-Funktion Werte zu.

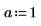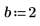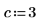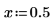2. Werten Sie die Funktion an fhyper(a,b,c,x) aus.

<region id="ID0EHNWCB" actualWidth="270.33000000000004" actualHeight="25.6" top="729.60000000000014" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">fhyper</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="15" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

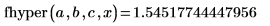
3. Stellen Sie sicher, dass die Funktion hypergeom dieselben Ergebnisse wie fhyper für den Spezialfall zurückgibt, für den gilt:

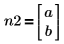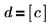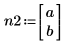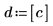<region id="ID0EZSWCB" actualWidth="346.40333333333336" actualHeight="39.2" top="787.20000000000016" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="49">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">hypergeom</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
        </sequence>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">float</id>
          <real>15</real>
        </sequence>
      </command>
      <symResult>
        <real>1.54517744447956</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Zugehörige Themen

Beta, Hypergeom und Zeta

Hypergeometrische Funktionen

War dies hilfreich?