Beispiel: Varianzanalyse für nicht replizierte Fakultäten
Verwenden Sie die Funktion anova, um eine Varianzanalyse für eine nicht replizierte Fakultät durchzuführen, indem ein nicht signifikanter Faktor erkannt und dann die Fakultät in eine Fakultät niedrigerer Ordnung projiziert wird.
1. Rufen Sie die Funktion fullfact auf, um eine Konstruktionsmatrix vollständiger Fakultät für ein Experiment zu erstellen, mit dem die Filtrationsrate einer Versuchsanlage getestet werden soll. Die Faktoren A, B, C und D stehen für die Temperatur, den Druck, die Konzentration von Formaldehyd und die Rührgeschwindigkeit.
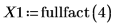
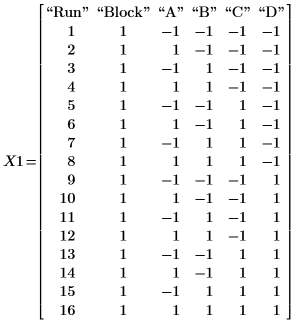
2. Zeichnen Sie die Ergebnisse des Experiments in der Matrix Y1 mit einem Element für jeden der sechzehn Rechenläufe auf.

3. Rufen Sie die Funktion quickscreen auf, um die mittlere Antwort für jeden Hauptfaktor zu erhalten.

4. Erstellen Sie ein Wirkungsdiagramm, um die signifikanten Faktoren zu bestimmen.
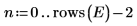
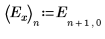
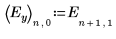
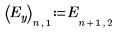

Der Faktor C und die Interaktionen zweiter Ordnung einschließlich C haben nur geringe Auswirkungen auf das Experiment. Im Vergleich zu den Faktoren A, B und D ist der Faktor C nicht signifikant.
5. Rufen Sie die Funktion anova auf, um eine Varianzanalyse durchzuführen.
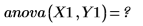
Die Funktion anova gibt einen Fehler zurück, da Y1 nicht repliziert wird. Da C nicht signifikant ist, sind “Run 1” und "Run 5" Duplikate, solange die Faktoren A, B und D beteiligt sind. Dies gilt ebenfalls für “Run 2" und "Run 6". Die gesamte Konstruktionsmatrix ABCD 24 enthält ein Duplikat der Konstruktionsmatrix ABD 23, wenn C nicht signifikant ist.
6. Rufen Sie die Funktion fullfact auf, um eine Konstruktionsmatrix 23 mit vollständiger Fakultät zu erzeugen.

In X2 sind die Faktornamen geändert. Die ursprünglichen Faktoren A, B, D werden zu A, B, C.
7. Ordnen Sie die Ergebnisse des Experiments für ein Experiment 23 mit vollständiger Fakultät neu an.
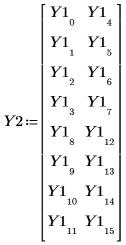
8. Rufen Sie die Funktion anova mit Y2 auf.
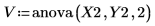
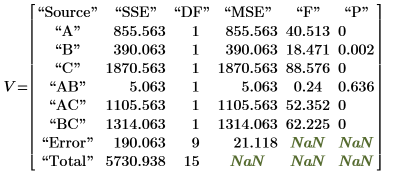
9. Verwenden Sie die Funktion qF, um den kritischen F-value für die Faktoren und Interaktionen zu berechnen und ihren F-value mit dem kritischen F-value zu vergleichen.
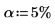
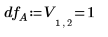
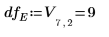
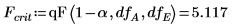
◦ Das Effektdiagramm zeigt an, dass Faktor C im Vergleich zu A, B und D nicht signifikant ist.
◦ Die Faktoren A, B, D (in V dargestellt als A, B, C) und ihre Interaktionen AD, BD (in V dargestellt als AC, BC) sind auf der 5-%-Ebene signifikant, da ihre F-values größer sind als Fcrit. Diese Varianzanalyse verstärkt die aus dem Wirkungsdiagramm abgeleitete subjektive Folgerung.
Verweis
Montgomery, D.C., Design and Analysis of Experiments, 5. Ausgabe, John Wiley & Sons, New York, 2001, S. 246 ff.