Beispiel: Varianzanalyse mit 1 Faktor
Verwenden Sie die Funktion fullfact, um ein Experiment zu konstruieren, und die Funktion anova, um das Ergebnis des Experiments zu analysieren.
1. Definieren Sie die Anzahl der Faktoren in einem Experiment, dass die Auswirkung des Baumwollfaseranteils auf die Stärke einer neuen Synthetikfaser testet.
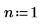
2. Definieren Sie die im Experiment verwendeten Einstellungen für die Baumwolle.
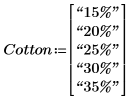
3. Verwenden Sie die Funktion length, um die Anzahl der Ebenen für den Faktor festzulegen.
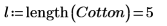
4. Rufen Sie die Funktion fullfact auf, um eine vollständige Fakultäten-Konstruktionsmatrix zu erstellen, die das Experiment und seine Durchläufe darstellt.
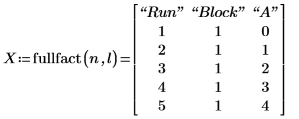
In der Konstruktionsmatrix X steht A für den Baumwollfaktor, und die Ebenen werden codiert dargestellt:
Codierte Werte von A | Reelle Werte von A |
|---|---|
0 | 15 % |
1 | 20 % |
2 | 25 % |
3 | 30 % |
4 | 35 % |
5. Messen Sie die Stärke der Synthetikfaser beim ersten Durchlauf, wenn der Anteil der Baumwollfaser 15 % beträgt.
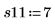
6. Erfassen Sie Messwerte für die übrigen vier Durchläufe.
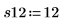
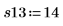
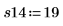
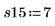
7. Rufen Sie die Funktion randomize auf, um die Reihenfolge der Durchläufe zufällig zu ändern.
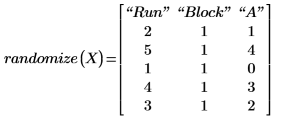
8. Replizieren Sie die Messungen in der von der Funktion randomize vorgegebenen Reihenfolge.
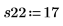
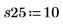
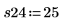
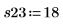
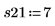
Die Experimente zu wiederholen kann den Effekt nicht steuerbarer Variablen ausgleichen. Wenn Sie die Funktion randomize aufrufen, bevor Sie die Experimente wiederholen, können Sie so die Ordnung der Korrelation zwischen den Eingabefaktoren verringern.
9. Wiederholen Sie die Schritte 7 und 8 für alle gewünschten Replikate. Erfassen Sie alle Messwerte in der Matrix Y.

Jede Spalte enthält die Daten eines der Replikate, und jede Zeile enthält die Daten eines bestimmten Durchlaufs.
10. Rufen Sie die Funktion boxplot auf, um die Daten für ein Boxplot aufzubereiten, das ein Feld für jeden Durchlauf aufweist.
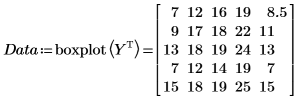
Die Matrix Y wird transponiert, da die Ergebnisse aller Durchläufe in Matrixzeilen erfasst werden, die in boxplot eingegebenen Datensätze jedoch Matrixspalten sein müssen.
11. Rufen Sie die Funktion boxplotgraph auf.
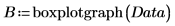
12. Erstellen Sie ein Boxplot.
a. Plotten Sie die Ausgabe der Funktion boxplotgraph:
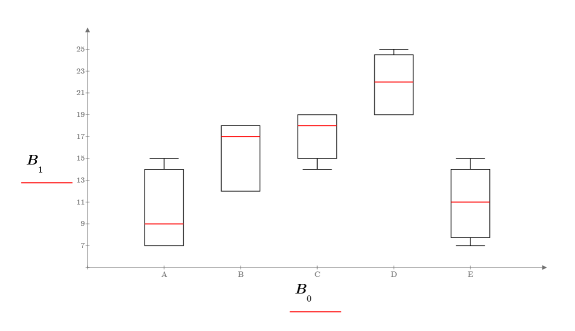
b. Erstellen Sie Textbereiche mit den Beschriftungen für die einzelnen Faktoren:
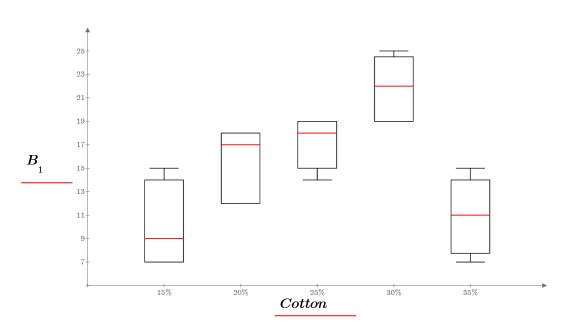
Beim Betrachten des Boxplots sieht es danach aus, dass der prozentuale Gewichtsanteil der Baumwolle die Zugstärke der Faser beeinflusst. Die Zugstärke der Faser erreicht ein Maximum, wenn der Baumwollanteil ca. 30 % des Fasergewichts beträgt.
13. Rufen Sie die Funktion anova auf, um zu testen, ob der prozentuale Gewichtsanteil der Baumwolle die Zugfestigkeit beeinflusst.

14. Definieren Sie r als Anzahl der Durchläufe und x als Anzahl der Replikate. Berechnen Sie dann die Summe der Quadrate in der Spalte SSE.
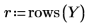
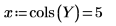
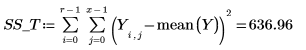
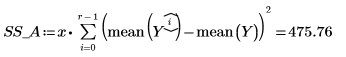
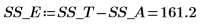
15. Definieren Sie N als Gesamtzahl der Messwerte, und berechnen Sie den Freiheitsgrad in der Spalte df.
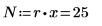
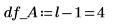
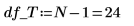
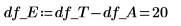
16. Berechnen Sie den Mittelwert der Quadrate in der Spalte MSE.
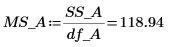
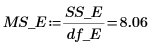
17. Berechnen Sie den F-value für den Faktor A.
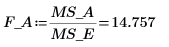
Der P-value in der Spalte P ist geringer als 0.05, was darauf hinweist, dass der Faktor A signifikant ist.
18. Verwenden Sie den F-value zum Testen der Hypothese, dass A ein signifikanter Faktor ist. Berechnen Sie den kritischen F-Wert für ein Signifikanzniveau von 5 %.
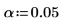
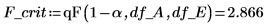
Der F-value für den Faktor A ist größer als der kritische F-Wert, wodurch erneut bestätigt wird, dass der prozentuale Gewichtsanteil der Baumwolle die Zugstärke der Faser beeinflusst.
Verweis
Montgomery, D.C., Design and Analysis of Experiments, 5. Ausgabe, John Wiley & Sons, New York, 2001. 62.