ODE 求解器
• 下面的每个函数均返回一个 (intvls+1)×(n+1) 解矩阵,其中 n 是未知量个数。矩阵的第一列包含 x 的值,在这些值所在处进行求解。这些值是 x1 和 x2 之间 (intvls + 1) 个等间隔的数。其余列包含解 y0, y1, ..., yn-1 的值,与第一列中 x 的值相对应。
• 对于求解器 rkfixed、RkAdapt、Bulstoer、Stiffb 和 Stiffr,在对其调用之前,您可以通过定义变量 TOL 来指定解的标量公差。例如,可将所有变量的公差设为 10-6:
TOL:=10-6
TOL 不会影响求解器 Adams、BDF 或 Radau 的公差。对于上述求解器,用户必须使用可选自变量 tol 来指定公差。
• 您可能希望使用 ODE 求解命令块来简化方程和初始条件的条目。
适用于非刚性方程组的求解器
• Adams(init, x1, x2, intvls, D, [tol]) - 使用 Adams 方法。
• rkfixed(init, x1, x2, intvls, D) - 使用四阶 Runge-Kutta 固定步长方法。
• Rkadapt(init, x1, x2, intvls, D) - 使用具有自适应步长的四阶 Runge-Kutta 方法。
• Bulstoer(init, x1, x2, intvls, D) - 使用比 Runge-Kutta 稍微更精确一些的 Bulirsch-Stoer 方法,但需要使用变化平滑的方程组。
适用于刚性方程组的求解器
使用这些函数来求解刚性或代数 ODE 问题。
• BDF(init, x1, x2, intvls, D, [J], [tol]) - 使用反微分公式法。可使用可选自变量 J 或 tol,同时忽略其他自变量。
• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) - 使用 Radau5 方法。可使用可选自变量 J、M 和 tol 的任意组合,同时忽略不希望使用的选项。
• Stiffb(init, x1, x2, intvls, D, AJ) - 使用 Bulirsch-Stoer 方法。
• Stiffr(init, x1, x2, intvls, D, AJ) - 使用 Rosenbrock 方法。
混合求解器
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) - 确定方程组为刚性方程组还是非刚性方程组,并相应调用 Adams 或 BDF。可使用可选自变量 J 或 tol,同时忽略其他自变量。
自变量
• 如果是单个 ODE,init 为 n 个实数初始值所组成的矢量 (其中,n 为未知量的个数),或是单个标量初始值。
• x1 和 x2 是求解 ODE 时所对应区间的实标量端点。init 中的初始值是在 x1 处所求的 ODE 函数的值。
• intvls 是用来插入解函数的离散区间的整数个数。解点的个数就是间隔数 + 1。
• D 是形如 D(x,y) 的矢量函数,用于指定方程组右侧的内容。
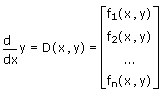
• tol (可选) 为实数值或实数值矢量,用于指定系统中每个自变量的公差。公差为解变量所需达到的精度。
◦ 应该将 tol 设为小于或等于 10-5。根据问题的规模,以及所使用的相对步长大小,可能需要减小 TOL 的值以获得合适的解。tol 的值越小,求解器算法达到所需精度的执行步数便越多。
◦ 求解方程组时,如果将 tol 设置为标量,会为方程组中的所有变量指定同一公差。如果将 tol 设置为矢量 (其长度等于方程组中的变量数),会分别为每个变量指定公差。
• J (可选) 为形如 J(x, y) 的函数,它返回雅可比矩阵,即:D 中函数关于 y0, y1, ... yn-1 的偏导数矩阵。
• M (可选) 为表示 M · dy/dt = f(t, y) 形式的变量之间的任意耦合的实矩阵。
• AJ 为形如 AJ(x, y) 的函数,它返回扩展雅可比行列式,该行列式的首行包含方程组右侧函数关于 x 的偏导数。其余列为雅可比行列式 J 的列,它包含关于 y0, y, ... yn-1 的偏导数。
D、J 和 AJ 函数用于不带自变量的求解器;函数 yn(x) 在 D、J 和 AJ 中指定,且不带自变量。
即使此处仅有一项,D、J 和 AJ 的第二个自变量也必须以矢量作为下标。
附加信息
• 在求解微分方程时,函数 Radau 和 Rkadapt 会在内部使用大小不一致的步长,这样,会在解变化较大的区域中添加更多的步长,但是会返回在 intvls 中所指定的等间隔点数量的解。
• 使用 Radau 的好处之一是无需输入雅可比行列式,尽管使用 J (如果可用) 可提高精度。