关于微分方程求解器
常微分方程 (ODE) 求解器可求解一个变量的未知函数的方程或方程组。偏微分方程 (PDE) 求解器可求解两个变量的函数 (1D PDE)。
常微分方程
要直接求解 ODE 而不创建求解命令块,请使用其中一种 ODE 求解器,它可求解以下形式的 ODE 方程组:
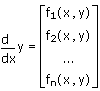
其中,y 为由自变量 x 的未知函数所组成的矢量。要求解高阶 ODE,请将其修改为一阶 ODE 方程组。
ODE 求解器分为两种:用于刚性方程组的求解器和用于非刚性方程组的求解器。以 y’=Ay 矩阵形式所编写的 ODE 方程组,如果矩阵 A 为近似奇异矩阵,则其称为刚性方程组。否则,为非刚性方程组。
• Adams - Adams-Bashford 法
• rkfixed, Rkadapt, Bulstoer - 四阶 Runge Kutta 算法 (具有固定步长和自适应步长) 和用于平滑变化 ODE 的 Bulstoer 法
• BDF - 反微分公式法
• Radau, Stiffb, Stiffr - RADAU、Bulirsch-Stoer 和 Rosenbrock 法,适用于刚性方程组
• statespace - 线性、一阶 ODE 方程组
• bvalfit, sbval - 边界值问题 (并非所有初始条件都是已知的),已通过线性抛射将其转换为初始值问题
还存在各种特殊的多项式生成器和超几何函数,用于求解特定 ODE 和普通 ODE。
偏微分方程
• numol - 命令行求解器,适用于 1D PDE 双曲线方程组和抛物线方程组,包括耦合的 ODE 和代数约束
• relax, multigrid - 命令行求解器,适用于泊松/拉普拉斯的椭圆 PDE
• numol 用于求解瞬变 1D 双曲线和抛物线 PDE (x, t 函数)。
• multigrid 用于在方形区域上求解稳态 2D 椭圆 PDE (x, y 函数)。
雅可比
• Jacob - 返回矢量的雅克比矩阵。