数据的离散傅立叶变换
• dft(A), idft(Z) - 返回复数值矢量或矩阵的正/逆傅立叶变换。
如果 dft 的输入是长度为 r 的矢量 V,则︰
◦ dft(V) 的输出是长度为 r 的矢量 Z。
◦ idft(Z) 的输出是长度为 r 的矢量。
如果 dft 的输入是有 r 行和 c 列的矩阵 M,则︰
◦ dft(M) 的输出是有 r 行和 c 列的矩阵 P。
◦ idft(P) 的输出是有 r 行和 c 列的矩阵。
• dftr(B), idftr(Z) - 返回实数值矢量或矩阵的正/逆傅立叶变换。
如果 dftr 的输入是长度为 r 的矢量 V,则︰
◦ dftr(V) 的输出是长度为 Z 的矢量 L,其中 L=floor(r/2)+1。Z 的各个元素与 dft(V) 输出的前 L 个元素完全相同。
◦ idftr(Z) 的输出是长度为 r=2(L-1) 的矢量。
如果 dftr 的输入是有 r 行和 c 列的矩阵 M,则︰
◦ dftr(M) 的输出是有 P 行和 r 列的矩阵 L,其中 L=floor(c/2)+1。P 的各个元素与 dft(M) 输出的前 L 列完全相同。
◦ idftr(P) 的输出是有 r 行和 c=2(L-1) 列的矩阵。
自变量
• A 为任意大小的复数值矢量或矩阵。
• B 为实值矢量或矩阵。忽略所有虚数部分。如果 B 是矢量,则行数必须是 2 的倍数。如果 B 是矩阵,则列数必须是 2 的倍数。
• 对于 A 和 B,数据必须具有兼容的单位
矢量的傅立叶变换
• 如果 A 是一个大小为 m 的矢量,则矢量 A 的一维 (1D) 正变换的第 u 个元素由 Zu 给出,如下所示:
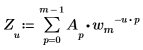
其中:
◦ m 为行号,而 u 则定义为: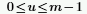
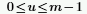
◦ i 为虚数单位,而 wm 则定义为:
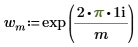
计算以上定义中的 Z 等同于将 dft 函数应用于矢量 A。
• 如果 Z 是一个大小为 m 的矢量,则矢量 Z 的一维 (1D) 逆变换的第 u 个元素由 Au 给出,如下所示:
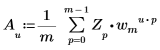
其中:
◦ m、u 和 wm 已在上文进行了定义。
计算以上定义中的 A 等同于将 idft 函数应用于矢量 Z。
矩阵的傅立叶变换
• 如果 A 是一个大小为 mxn 的矩阵,则矩阵 A 的二维 (2D) 正变换的第 (u,v) 个元素由 Zu,v 给出,如下所示:
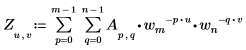
其中:
◦ m、u 和 wm 已在上文进行了定义。
◦ n 为列号,而 v 则定义为: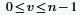
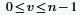
◦ i 为虚数单位,而 wn 则定义为:
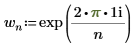
计算以上定义中的 Z 等同于将 dft 函数应用于矩阵 A。
• 如果 Z 是一个大小为 mxn 的矩阵,则矩阵 A 的二维 (2D) 逆变换的第 (u,v) 个元素由 Au,v 给出,如下所示:
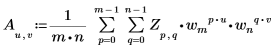
其中:
◦ m、n、u、v、wm 和 wn 已在上文进行了定义。
计算以上定义中的 A 等同于将 idft 函数应用于矩阵 Z。
附加信息
• 当矢量行数和矩阵列数为 2 的幂时,傅里叶函数运行更快。
• 新 dft/idft 函数取代已弃用 cfft/icfft 和 CFFT/ICFFT 函数的功能,并具有显著性能改进,尤其对于较大的数据集和大小非 2 的幂的情况。
• 新 dftr/idftr 函数取代已弃用 fft/ifft 和 FFT/IFFT 函数的功能。
函数 dftr 作用于长度为偶数的实矢量和具有偶数列的矩阵。
• 函数 fft/FFT 仅作用于长度为 2 的幂的实矢量。
• 函数 ifft/IFFT 仅为输入矢量长度的一半加一,或者为 2k-1+1,其中 k 为大于 1 的整数。另一半是第一部分的反向共轭,必须手动重新构建这一半。函数 dft/idft 返回完整的结果。
• 在缩放因子和指数符号方面,函数 dft/idft 不同于已弃用的 fft/ifft、FFT/IFFT、cfft/icfft 和 CFFT/ICFFT。
◦ 对于正变换,差异为:
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
缩放因子 | 1 | 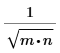 | 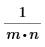 |
指数符号 | 负数 | 正数 | 负数 |
◦ 对于逆变换,差异为:
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
缩放因子 | 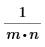 | 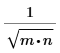 | 1 |
指数符号 | 正数 | 负数 | 正数 |
当针对仅作用于矢量 (1D 情况) 的函数计算缩放因子时,假定 n=1。