무한 극한을 사용하는 적분 수치 연산 비수렴
이 항목에서는 무한 통합 극한 1~2개를 사용하는 적분 수치 연산 시 발생하는 두 가지 비수렴 오류 사례를 해결하는 방법을 설명합니다.
여기서는 이 두 사례를 파악하기 위해 평균 μ 및 표준 편차 σ를 정의합니다.
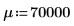
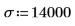
사례 1: 무한 통합 극한 하나를 사용하는 적분
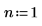
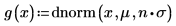
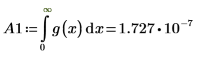
n=1일 때 [0, ∞] 범위에서 g(x) 적분 연산을 수행하면 오류가 반환되지는 않지만 매우 작은 값이 반환됩니다.
사례 1을 해결하는 방법
n의 값을 n=2로 늘리고 적분 연산을 다시 수행합니다.
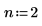
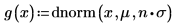
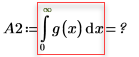
n 값을 n=2로 늘리면 계산이 해로 수렴되지 않으므로 오류가 발생합니다.
이 오류를 해결하려면 g(x)의 tail에 가까운 값으로 T 변수를 설정한 다음 적분 하나를 범위 [0, T] 및 [T, ∞]가 각각 포함되는 두 개로 분할합니다.
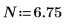 | 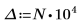 |
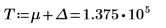 |
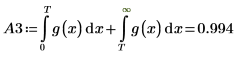
분할된 적분 A3는 n=1 또는 n=2에서 모두 적절한 응답을 반환합니다. g(x)의 도표를 만든 다음 세로 마커 T를 추가하면 적분이 g(x)의 tail과 어느 정도 가까운지를 확인할 수 있습니다.
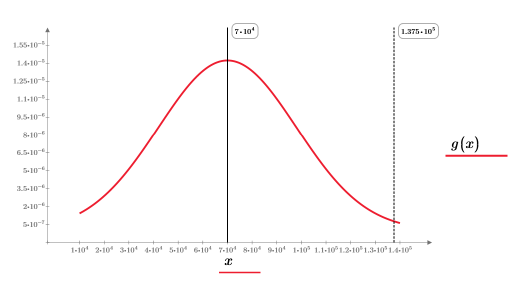
도표에는 T 변수가 g(x)의 tail에 가까운 세로 마커로 표시됩니다.
사례 2: 무한 통합 극한 두 개를 사용하는 적분
승수 변수 n을 1로 설정한 다음 [-∞, ∞] 범위에서 g(x)의 적분 연산을 수행합니다.
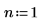
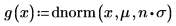
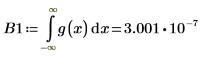
n=1일 때 [-∞, ∞] 범위에서g(x) 적분 연산을 수행하면 오류가 반환되지는 않지만 매우 작은 값이 반환됩니다.
사례 2를 해결하는 방법
이 오류를 해결하려면 g(x)의 head 및 tail에 가까운 값으로 T1 및 T2 변수를 설정한 다음 적분 하나를 범위 [-∞, T1], [T1, T2], [T2, ∞]가 각각 포함되는 세 개로 분할합니다.
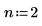
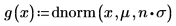
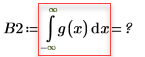
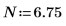 | 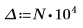 |
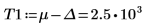 | 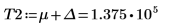 |
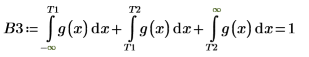
분할된 적분은 n=1 또는 n=2에서 모두 적절한 응답을 반환합니다. g(x)의 도표를 만든 다음 세로 마커 T1및 T2를 추가하면 적분이 g(x)의 head 및 tail과 어느 정도 가까운지를 확인할 수 있습니다.
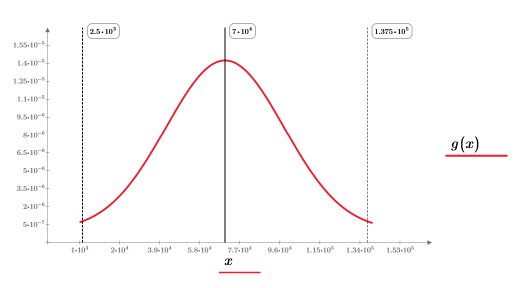
관찰 및 결론
평균은 같지만 각기 다른 두 표준 편차 값을 사용하여 기본 제공 확률 밀도 함수 dnorm의 도표를 만듭니다.
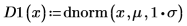
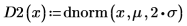
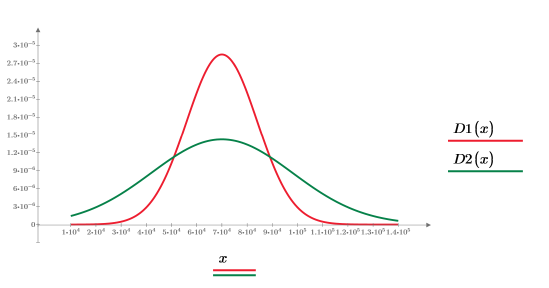
도표에는 다음 내용이 표시됩니다.
• 표준 편차 값을 줄이면 곡선 아래 영역 대부분이 평균에 가까워집니다. 이 경우 숫자 계산은 수렴되지만 잘못된 응답이 반환됩니다.
• 표준 편차 값을 늘리면 곡선 아래 영역 대부분이 평균에서 멀어지도록 분산됩니다. 이 경우에는 숫자 계산이 수렴되지 않습니다.
두 경우 모두 적분을 분할하면 계산이 수렴되며 올바른 응답이 반환됩니다.