예제: 확률 분포

함수 > 통계 > 확률 분포 > 예제: 확률 분포

예제: 확률 분포

확률 분포 표 대신 확률 분포 함수를 사용합니다.

확률 밀도

1. dchisq 함수를 사용하여 5.5에서 자유도 11인 카이제곱 변수의 확률 밀도를 계산합니다.

2. dt 함수를 사용하여 -1.56에서 자유도 4인 t 변수의 확률 밀도를 계산합니다.

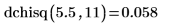
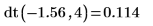
누적 확률

1. pnorm 함수를 사용하여 표준 정규 변수가 1.0을 넘을 확률을 계산합니다.

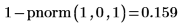
2. pchisq 함수를 사용하여 자유도가 7인 카이제곱 변수가 5.6보다 작을 확률을 계산합니다.

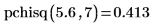
3. pbinom 함수를 사용하여 크기가 15이고 매개변수가 0.6인 이항 변수가 10보다 작거나 같을 확률을 계산합니다.

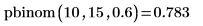
4. qbinom 함수를 사용하여 크기가 15이고 매개변수가 0.6인 이항 변수가 10보다 작거나 같을 확률을 계산합니다.

5. rbinom 함수를 사용하여 크기가 n=7이고 성공할 확률이 q=0.65인 이항 분포에 따라 난수 m=5개의 벡터를 생성합니다.

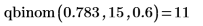
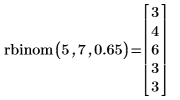
워크시트를 다시 계산하면 rbinom 함수가 새 난수 집합을 구합니다.

6. dbeta 함수를 사용하여 실수 형상 매개변수 3 및 2에 대한 값 x=0.8의 확률 밀도를 계산합니다.

7. pbeta 함수를 사용하여 a=3이고 b=2인 베타 변수가 0.8을 초과할 확률을 계산합니다.

8. qbeta 함수를 사용하여 확률 p=0.8의 역 누적 확률 분포를 계산합니다.

9. rbeta 함수를 사용하여 크기가 n=6이고 성공할 확률이 q=0.75인 이항 분포에 따라 난수 m=5개의 벡터를 생성합니다.

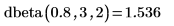
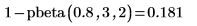
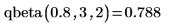
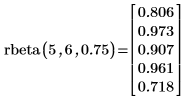
역 누적 확률

1. qnorm 함수를 사용하여 확률 p의 역 누적 확률 분포를 계산합니다.

2. qt 함수를 사용하여 확률 p의 역 누적 확률 분포를 계산합니다.

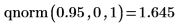
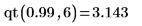
F 분포

1. dF 함수를 사용하여 자유도가 4와 6인 F 분포의 65번째 백분위수를 계산합니다.

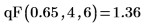
2. pF 함수를 사용하여 자유도가 5와 7인 0.75 확률의 누적 확률 분포를 계산합니다.

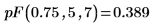
3. qF 함수를 사용하여 자유도가 9와 8인 F 분포의 95번째 백분위수를 계산합니다.

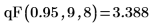
4. rF 함수를 사용하여 자유도가 2와 3인 F 분포에 따라 난수 7개의 벡터를 생성합니다.

워크시트를 다시 계산하면 rF 함수가 새 난수 집합을 구합니다.