Décomposition d'une valeur singulière (SVD)
• svds(A) : renvoie un vecteur contenant les valeurs singulières de A, les racines carrées positives des eigenvalues de la matrice AH·A, où AH est la transposée conjuguée de A. Vous pouvez calculer AH en utilisant les opérateurs transpose et complex conjugate comme suit.
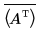
• svd(A) : renvoie un vecteur de 3 tableaux imbriqués.
Le premier tableau contient le vecteur s des valeurs singulières renvoyées par svds. Les deux tableaux suivants sont des matrices U et VH respectant A = U∙diag(s)·VH. La troisième entrée VH est la transposée conjuguée de V.
Le troisième tableau est VH et non V. Cela signifie que la transposée conjuguée a déjà été appliquée au tableau renvoyé. Il n'est pas nécessaire de l'appliquer à nouveau. Vous pouvez utiliser le tableau renvoyé directement dans la formule.
Arguments
• A est un tableau m × n, où m ≥ n. Pour svd, les éléments du tableau doivent être des nombres réels ; pour svds, les valeurs complexes sont autorisées.
Informations supplémentaires
• Les valeurs singulières sont toujours réelles et positives. Les très petites valeurs doivent être interprétées comme 0.
• La fonction svd utilise les bibliothèques Intel Basic Linear Algebra Subprograms (BLAS)/Linear Algebra Package (LAPACK).