• Chacune des fonctions ci-dessous renvoie une matrice de solutions (intvls+1)×(n+1), où n est le nombre d'inconnues. La première colonne de la matrice contient les valeurs de x pour lesquelles les solutions sont évaluées. Ces valeurs sont des (intvls + 1) nombres avec un espacement régulier entre x1 et x2. Les colonnes restantes contiennent les valeurs des solutions y0, y1, ..., yn-1 correspondant aux valeurs de x de la première colonne.

• Dans le cas des solveurs rkfixed, RkAdapt, Bulstoer, Stiffb et Stiffr, vous pouvez indiquer la tolérance scalaire de la solution en définissant la variable TOL avant d'appeler le solveur. Par exemple, vous pouvez définir la tolérance de toutes les variables à 10-6 :

• Vous pouvez utiliser les blocs de résolution d'EDO pour simplifier la saisie de vos équations et conditions initiales.

• Adams(init, x1, x2, intvls, D, [tol]) : utilise les méthodes Adams.

• rkfixed(init, x1, x2, intvls, D) : utilise la méthode Runge-Kutta du quatrième ordre à pas fixes.

• Rkadapt(init, x1, x2, intvls, D) : utilise la méthode de Runge-Kutta d'ordre quatre à pas adaptatif.

• Bulstoer(init, x1, x2, intvls, D) : utilise la méthode de Bulirsch-Stoer, qui est légèrement plus précise que la méthode de Runge-Kutta, mais qui nécessite un système variant de manière lente.

• BDF(init, x1, x2, intvls, D, [J], [tol]) : utilise des méthodes de différentiation rétrograde. Vous pouvez utiliser l'un ou l'autre des arguments facultatifs J ou tol et omettre l'autre.

• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) : utilise la méthode de Radau5. Vous pouvez utiliser toutes les combinaisons des arguments facultatifs J, M et tol, et omettre les options que vous ne souhaitez pas utiliser.

• Stiffb(init, x1, x2, intvls, D, AJ) : utilise la méthode de Bulirsch-Stoer.

• Stiffr(init, x1, x2, intvls, D, AJ) : utilise la méthode de Rosenbrock.

• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) : détermine si un système est raide ou non raide, et appelle Adams ou BDF en conséquence. Vous pouvez utiliser l'un ou l'autre des arguments facultatifs J ou tol et omettre l'autre.

• init est soit un vecteur de n valeurs initiales réelles, où n est le nombre d'inconnues, soit une valeur initiale scalaire unique dans le cas d'une EDO unique.

• x1 et x2 sont les bornes scalaires réelles de l'intervalle sur lequel la solution des EDO est évaluée. Les valeurs initiales dans init sont les valeurs des fonctions EDO évaluées à x1.

• intvls est le nombre entier d'intervalles de discrétisation utilisés pour interpoler la fonction de solution. Le nombre de points de solution est le nombre d'intervalles + 1.

• D est une fonction vectorielle de la forme D(x,y) définissant le côté droit du système.

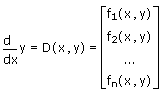
• tol (facultatif) est une valeur réelle ou un vecteur de valeurs réelles définissant la tolérance de chaque variable indépendante du système. La tolérance est la précision requise pour une variable de la solution.

◦ Vous devez définir tol comme étant inférieur ou égal à 10-5. Selon l'échelle du problème et le pas relatif utilisé, vous aurez peut-être besoin de réduire la valeur de TOL pour obtenir des solutions appropriées. Plus la valeur de tol est petite, plus l'algorithme du solveur effectuera de pas pour atteindre la précision requise.

◦ Si vous résolvez un système d'équations, la définition de tol comme scalaire indique la même tolérance pour toutes les variables du système. La définition de tol comme un vecteur de longueur égale au nombre de variables du système, indique des tolérances distinctes pour chacune des variables.

• J (facultatif) est une fonction de la forme J(x, y) qui renvoie la matrice jacobienne, à savoir la matrice des dérivées partielles des fonctions dans D par rapport à y0, y1, ... yn−1.

• M (facultatif) est une matrice réelle représentant tout couplage entre les variables de la forme M · dy/dt = f(t, y).

• AJ est une fonction de la forme AJ(x, y) qui renvoie le jacobien augmenté. Sa première colonne contient les dérivées partielles par rapport à x des fonctions situées dans la partie droite du système. Les colonnes restantes sont les colonnes du jacobien J, contenant les dérivées partielles par rapport à y0, y1, ... yn−1.

• Les fonctions Radau et Rkadapt utilisent des incréments non uniformes au niveau interne lors de la résolution de l'équation différentielle, en ajoutant plus d'incréments dans les zones de plus grande variation de la solution, mais renvoient la solution à des points équidistants indiqués dans intvls.

• L'avantage d'utiliser Radau est qu'aucune entrée jacobienne symbolique n'est nécessaire, mais si J est disponible, son utilisation a tendance à améliorer la précision.