Dérivation de conditions initiales d'une équation différentielle ordinaire
Les fonctions suivantes sont utilisées en cas de problèmes aux valeurs limites, où certaines conditions initiales sont inconnues.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
Renvoie un vecteur contenant les valeurs initiales restant non définies à x1 pour l'équation différentielle ordinaire ou le système d'équations différentielles ordinaires identifiées dans D. Ces valeurs initiales peuvent alors être utilisées dans une des fonctions de résolution d'équations différentielles ordinaires. Si vous connaissez certaines valeurs de la solution et ses n − 1 premières dérivées à une valeur intermédiaire, utilisez bvalfit qui est particulièrement utile lorsque la dérivée est discontinue quelque part dans l'intervalle d'intégration. Si vous connaissez certaines valeurs au point initial et au point terminal, utilisez sbval. Le problème de valeur aux limites se transforme en problème de valeur initiale en effectuant des projections à partir des extrémités et en mettant en correspondance les trajectoires de la solution et de ses dérivées à un point intermédiaire.
Arguments
• v1, v2 sont des vecteurs d'estimations réelles pour les valeurs initiales manquantes en x1.
• x1, x2 sont les bornes réelles de l'intervalle sur lequel la solution des équations différentielles doit être évaluée.
• xf est un point intermédiaire réel entre x1 et x2 pour lequel les trajectoires des solutions doivent être égales.
• D(x, y) est une fonction évaluée par un vecteur de n éléments de la variable indépendante x et d'un vecteur de fonctions y, ce vecteur contenant les équations des dérivées premières de toutes les fonctions inconnues du système d'équations différentielles ordinaires.
Pour créer ce vecteur, convertissez votre ou vos équations en plaçant un terme de dérivée première seul du côté gauche, sans multiplicateur ni aucune dérivée d'ordre supérieur dans l'équation. Par exemple, une EDO unique de la fonction y(x) contenant une dérivée seconde doit être écrite sous la forme d'un système d'équations en y0(x) et yl(x), la dérivée première de y0 étant yl. L'EDO à fonction unique suivante est réécrite pour le solveur, en utilisant les indices vectoriels :
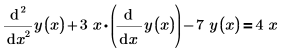
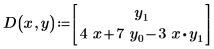 | avec côté gauche implicite | 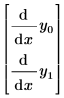 |
• load1(x1, v1), load2(x2, v2) sont des fonctions vectorielles réelles dont les éléments correspondent aux valeurs de yn à x1 et x2, respectivement. Certaines de ces valeurs seront des conditions initiales connues. Les valeurs inconnues sont les valeurs initiales correspondantes issues de v1 et v2, respectivement.
• scoreb(xf, y) est une fonction vectorielle réelle utilisée pour définir la façon dont vous souhaitez que les solutions soient conformes en xf. En général, vous définirez scoreb(xf, y):= y afin que les solutions de toutes les fonctions inconnues soient conformes en xf.
• scorei(x2, y) est une fonction vectorielle réelle dotée du même nombre d'éléments que v. Chacun de ces éléments correspond à la différence entre une valeur initiale en x2, telle qu'elle a été donnée, et l'estimation correspondante à partir de la fonction de résolution. Le vecteur score mesure avec quelle précision la solution proposée concorde avec les conditions initiales en x2. Une valeur 0 (zéro) pour un élément indique une concordance parfaite.