Exemple : Qualité de l'ajustement
Utilisez les fonctions polyfit et polyfitstat pour effectuer une régression linéaire et une analyse de la variance afin de tester la qualité de l'ajustement.
1. Définissez un tableau de données expérimentales relatif à un procédé de fabrication d'un polymère. La température de la réaction t et la vitesse d'alimentation en catalyseur fr affectent la viscosité vy du polymère.

alité de l'ajustement
2. Appelez la fonction polyfit afin de modéliser les données sous la forme d'une régression linéaire.
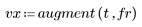
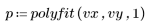
3. Calculez la viscosité prédite pour chaque valeur de la température et de la vitesse d'alimentation.
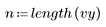
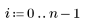
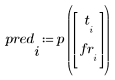
4. Calculez les résiduels (différence entre les valeurs calculées par le modèle et les valeurs mesurées).
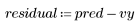
5. Tracez les résiduels par rapport à la viscosité, la température et la vitesse d'alimentation observées.
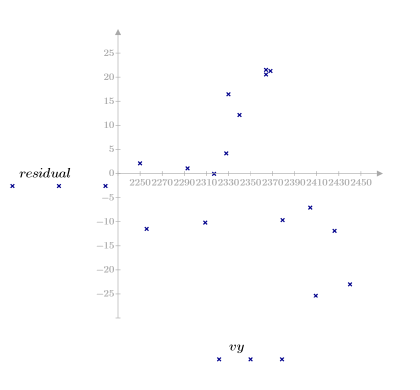
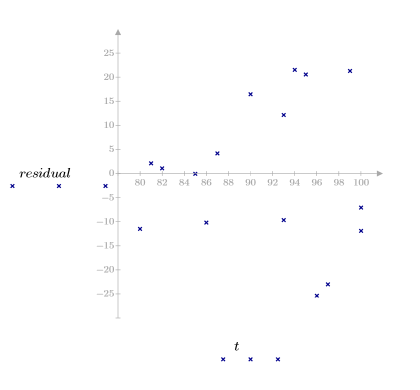
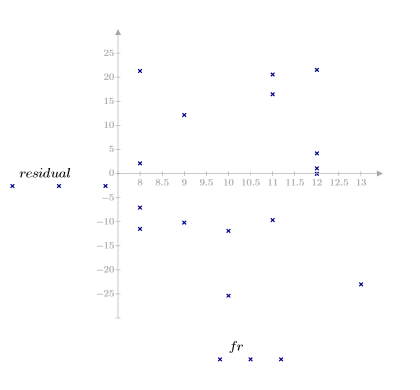
Les tracés des résiduels indiquent que les variances de la viscosité et de la température observées augmentent selon l'accroissement, respectivement, de la viscosité et de la température.
6. Appelez polyfitstat pour calculer les différentes statistiques du modèle linéaire. Affichez la matrice ANOVA renvoyée par la fonction polyfitstat à la ligne 8.
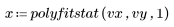
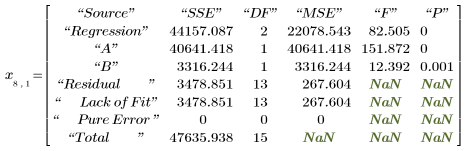
Dans la matrice ANOVA, les sources de la variance sont divisées entre les composants de régression et de résiduels. Le composant de régression est par ailleurs divisé entre chaque coefficient de régression. Vous ne pouvez cependant pas faire la différence entre le manque d'ajustement et l'erreur pure pour le résiduel car les résultats de l'expérience vy ne comportent pas de répliques.
Calcul et utilisation de la table ANOVA pour la régression
1. Calculez la somme des carrés due à l'erreur (SSE).
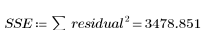
La SSE est égale à χ2, qui est une mesure métrique générale d'adéquation de l'ajustement. Elle correspond à la quantité réduite lors du calcul d'une solution à l'aide de la méthode des moindres carrés. L'erreur correspond à une mesure qui indique la façon dont le modèle s'ajuste aux données. Elle indique dans quelle mesure la déviation n'est pas expliquée par la régression.
2. Définissez les degrés de liberté de l'erreur df_error par rapport aux degrés de liberté totaux df_total et aux degrés de liberté des paramètres df_param. Les degrés de liberté correspondent à la longueur des données, moins le nombre de paramètres d'ajustement.
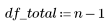
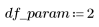
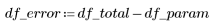
3. Définissez la somme des carrés due à la régression (SSR) par rapport à la somme totale des carrés (SST).
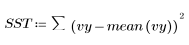
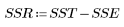
4. Définissez l'erreur de carré moyenne (MSE) et l'erreur moyenne de régression (MSR). Divisez l'erreur par les degrés de liberté appropriés.
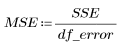
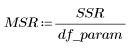
5. Réalisez une analyse du tableau de la variance afin de caractériser l'ajustement.
Somme des carrés | DF | Carré moyen | Facteur F | |
|---|---|---|---|---|
Régression | 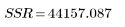 | 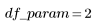 | 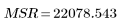 | 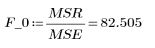 |
Erreur | 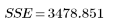 | 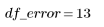 | 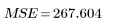 | |
Total | 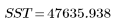 | 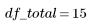 |
Vous pouvez comparer le tableau ci-dessus avec la matrice ANOVA polyfitstat.
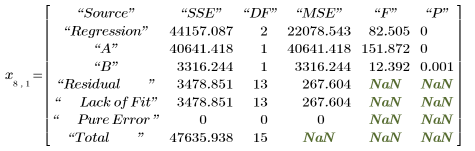
6. Estimez dans quelle mesure le modèle s'ajuste aux données :
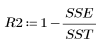
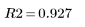
Ceci indique que 92.7 % de la variabilité de la viscosité s'explique par le modèle de régression linéaire appliqué.
7. Définissez le niveau de signification d'un test d'hypothèse afin de tester l'ajustement du modèle aux données.
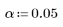
8. Calculez la valeur critique F.
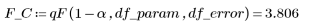
9. Testez l'hypothèse selon laquelle le modèle est ajusté aux données.
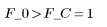
Acceptez l'hypothèse. Vous pouvez prévoir la viscosité du polymère grâce à ce modèle de régression linéaire.
Référence
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, pp. 398