Statistiques de régression polynomiale multivariée
• polyfitstat(X, Y, n/"terms"/M, [conf]) : renvoie les données statistiques relatives à un modèle de régression polynomiale adaptant les résultats enregistrés dans la matrice Y aux données trouvées dans la matrice X. Vous pouvez définir l'équation de régression polynomiale par son degré polynomial n ou par ses termes spécifiés dans la chaîne “terms” ou dans la matrice M. Utilisez la matrice M lorsque vous ne voulez pas inclure l'intercept dans l'ajustement polynomial. Utilisez l'argument facultatif conf pour spécifier un intervalle de confiance autre que la valeur par défaut de 95 %.
La deuxième colonne de la matrice renvoyée par polyfitstat contient les éléments suivants :
|
Ligne
|
Description
|
|---|---|
|
1
|
L'écart-type pour Y
|
|
2, 3, 4
|
R2, R2 ajusté et R2 prévu
|
|
5
|
PRESS : erreur de prévision de la somme des carrés (utile pour la mise à l'échelle des résiduels)
|
|
6
|
Statistique de test de Durbin-Watson pour l'autocorrélation
|
|
7
|
Matrice des coefficients de régression renvoyée par polyfitc
|
|
8
|
Matrice de la méthode ANOVA pour le modèle de régression avec des colonnes identiques à la table des résultats renvoyée par anova et avec les lignes suivantes :
• Régression : sous-total, qui est alors divisé pour chaque terme (à l'exception d'intercept)
• Résiduel (erreur) : sous-total, qui est alors divisé entre l'erreur de manque d'ajustement et l'erreur expérimentale pure
• Total pour le modèle de régression
|
|
9
|
Matrice des diagnostics avec les colonnes suivantes :
1. Numérotation pour chaque analyse ou point de données
2. Résultat observé pour chaque analyse ou point de données
3. Résultat prévu par le modèle de régression à l'examen
4. Résiduel : différence entre le résultat observé et le résultat prévu
5. Effet de levier : mesure de la distance entre le résultat observé et le point situé au centre de tous les résultats observés.
6. Résiduel de Student : résiduel divisé par la variance en fonction du résultat observé
7. R-student : résiduel divisé par la variance en fonction d'un jeu de données d'où le résultat observé a été supprimé
8. Distance de Cook : mesure de l'influence du résultat observé sur tous les autres points de données
9. DFFITS : différence entre le résultat prévu par un modèle de régression reposant sur un jeu de données dans lequel le résultat observé est inclus et le résultat prévu par un autre modèle d'où le résultat observé a été supprimé
|
Arguments
• X est une matrice d'expérience ou une matrice dans laquelle chaque colonne représente une variable indépendante. Chaque colonne de X doit avoir des unités compatibles.
• Y est un vecteur ou une matrice de résultats mesurés ou simulés, chaque ligne contenant les résultats de chaque exécution ou point de données défini dans X. Lorsque toutes lignes ne contiennent pas le même nombre de répliques, vous devez remplir les éléments vides de Y avec des NaN. Les éléments de Y doivent avoir des unités compatibles.
• n est un entier qui spécifie le degré polynomial. Il doit être inférieur au nombre total de points de données : 1 ≤ n ≤ length(Y) − 1. Dans le cas contraire, le problème ne présente pas de solution unique.
• “terms” est une chaîne qui spécifie les termes, ou les facteurs et interactions, à inclure dans le polynôme. "A B AB AA BB" signifie que la régression polynomiale contient les éléments suivants :
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
Pour les séparateurs, vous pouvez utiliser un espace, une virgule, un caractère deux points ou un caractère point-virgule.
• M est une matrice qui spécifie un polynôme avec des valeurs initiales des coefficients dans la première colonne et la puissance des variables indépendantes pour chaque terme dans les colonnes restantes. Pour le polynôme décrit ci-dessus, définissez M de la manière suivante :
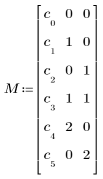
• conf (facultatif) est la limite de confiance souhaitée, un pourcentage exprimé comme nombre entre 0 et 1 inclus. Par défaut, conf = 0.95 pour un intervalle de confiance de 95 %.