Exemple : Oscillation harmonique amortie dans des circuits
Etant donné un circuit électrique simple contenant une résistance R, une bobine d'induction L et un condensateur C.
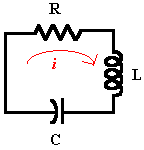
Utilisez des équations différentielles pour modéliser la charge Q sur le condensateur C, puis utilisez les fonctions de solveur d'EDO pour trouver d'autres solutions approximatives. Enfin, comparez les résultats à la solution exacte de Q.
Utilisation d'équations différentielles
1. Ecrivez une équation différentielle pour la tension des trois composants dont le total doit être égal à zéro.
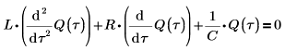
2. Ecrivez l'équation différentielle correspondant au changement instantané de charge Q sur le condensateur C :
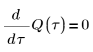
3. Définissez la charge Q au moment zéro :
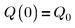
4. Partez des valeurs suivantes pour les paramètres d'entrée :
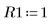
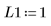
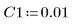
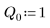
5. Transformez l'équation différentielle sous la forme standard :
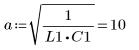
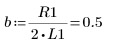
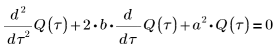
6. Résolvez l'équation pour tous les cas de a et de b :
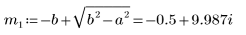
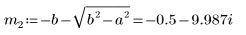
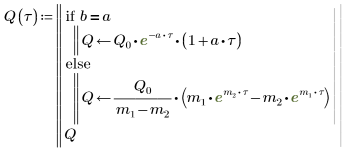
7. Tracez les deux solutions possibles pour Q :
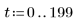
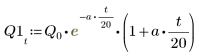
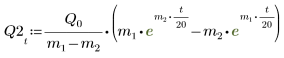
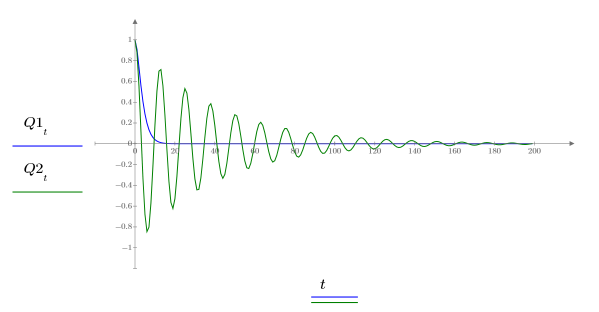
La charge Q1 tombe rapidement à zéro lorsque a=b, et oscille pendant un bon moment avant de passer à zéro quand a et b ne sont pas identiques.
Avant d'utiliser les solveurs d'EDO
• Définissez les paramètres à transmettre aux fonctions du solveur d'EDO :
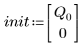 | 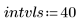 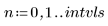 |
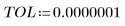 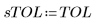 | 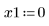 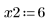 |
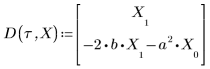 |
• Les solveurs d'EDO sont de deux types : ceux des systèmes raides et ceux des systèmes non raides. Un système d'EDO écrit sous forme matricielle, par exemple y' = Ax, est qualifié de raide si la matrice A est quasi singulière. Sinon, le système est non raide.
• La distinction entre systèmes raides et non raides peut être associée aux échelles de dynamique inhérentes de la matrice A telles que définies par ses valeurs propres. Une matrice dotée de valeurs propres disparates (ou de valeurs allant du trop petit au trop grand) constitue généralement un système raide.
• Selon les paramètres système spécifiés, ce simple exemple d'oscillation harmonique amortie représente un système non raide.
• Les fonctions Adams, AdamsBDF, BDF et Radau peuvent prendre une valeur spécifique de TOL ou utiliser leur propre valeur TOL par défaut de 10-5.
Utilisation de solveurs d'EDO pour systèmes non raides
Utilisez les solveurs d'EDO pour systèmes non raides pour trouver les solutions approximatives, puis comparez les résultats à la solution exacte de Q.
1. Adams
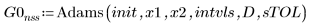
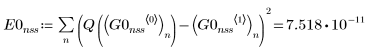
2. rkfixed
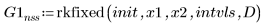
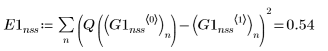
3. Rkadapt
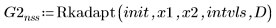
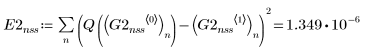
4. Bulstoer
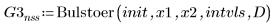
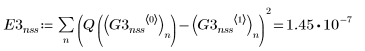
Utilisation de solveurs d'EDO pour systèmes raides
Utilisez les solveurs d'EDO pour systèmes raides pour trouver les solutions approximatives, puis comparez les résultats à la solution exacte de Q.
1. BDF
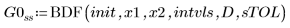
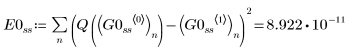
2. Radau
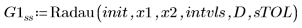
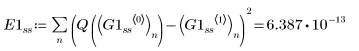
Utilisation du solveur hybride d'EDO
Utilisez le solveur hybride d'EDO AdamsBDF pour déterminer s'il s'agit d'un système raide ou non raide, puis appelez Adams ou BDF en conséquence pour trouver les solutions approximatives et comparer les résultats à la solution exacte de Q.
1. AdamsBDF
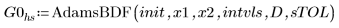
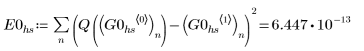
Conclusion
• Dans les solveurs d'EDO pour systèmes non raides, les fonctions Adams et rkfixed renvoient les solutions avec, respectivement, l'erreur la plus petite et l'erreur la plus grande.
• Dans les solveurs d'EDO pour systèmes raides, les fonctions Radau et BDF renvoient les solutions avec, respectivement, l'erreur la plus petite et la plus grande des deux.
• La fonction hybride AdamsBDF renvoie une valeur qui est la plus petite des deux valeurs renvoyées par Adams ou BDF.
• En règle générale, les fonctions Radau et rkfixed renvoient les solutions avec, respectivement, l'erreur la plus petite et l'erreur la plus grande.
Comparaison des résultats
1. Tracez les solutions renvoyées par les solveurs d'EDO pour les systèmes non raides avec les erreurs la plus petite (Adams, G0nss) et la plus grande (rkfixed, G1nss) :
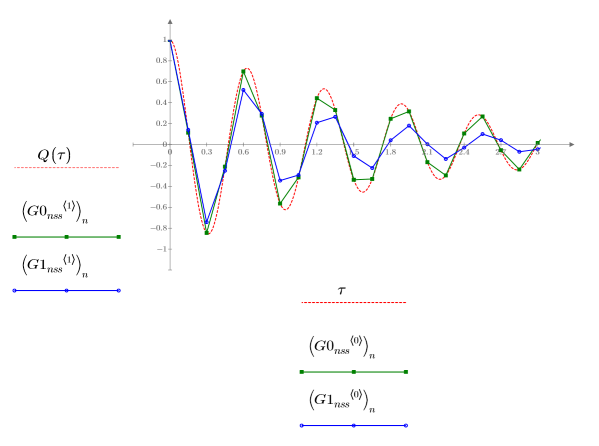
Ces deux solutions présentent des différences évidentes par rapport à Q.
2. Tracez les solutions renvoyées par les serveurs d'EDO pour les systèmes raides avec les erreurs la plus petite (Radau, G1ss) et la plus grande (BDF, G0ss) :
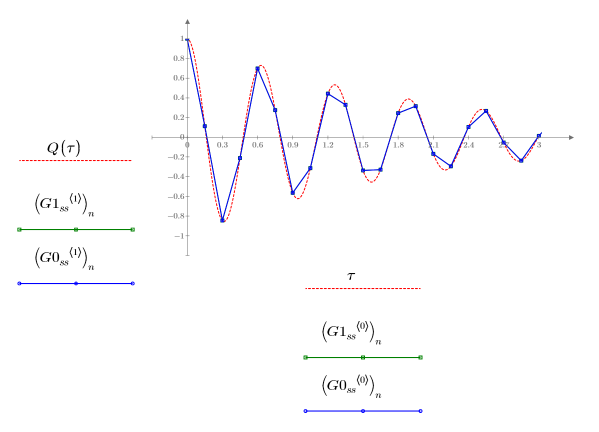
Les deux solutions semblent identiques par rapport à Q.
3. Tracez les solutions qui ont donné les erreurs la plus petite (Radau, G1ss) et la plus grande (rkfixed, G1nss), renvoyées par les solveurs d'EDO pour les systèmes raides et non raides :
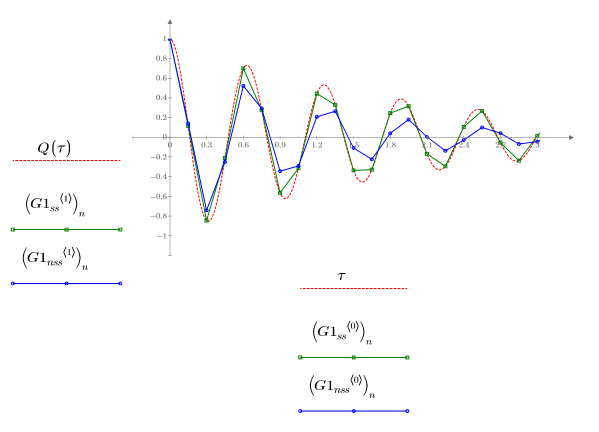
La fonction Radau, solveur de système raide, renvoie la meilleure approximation à la solution de Q.