Rational Function Regression
• rationalfit(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"])—Returns parameters and their confidence limits for a rational polynomial fit of order m and n on the top and bottom, or an allowable residual chi-squared, if the function should determine the optimal order. Confidence level conf is achieved, with optional standard deviations Stdy and optional lower and upper bounds on acceptable parameter values. If the optional string argument "noscale" is supplied, the input data is not scaled to the range 0 to 1 before calculating.
• rationalfitnp(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"])—Identical to rationalfit, but avoids poles in the resulting rational function. The default value for Acc is 10-7.
The rational fitting function is of the form:
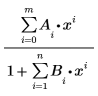
where m and n are the desired degree of the numerator and denominator respectively.
The output of rationalfit, or of rationalfitnp, is a three-column matrix, where the first column contains the values for the fitted parameters, and the second and third columns contain the left and right boundaries respectively, for the confidence interval on the parameters.
Arguments
• vx, vy are the vectors of real data values with the same length.
• conf is the desired confidence limit, a percentage expressed as a number between 0 and 1, inclusive.
• m, n are integer polynomial orders for the numerator and denominator of the rational function to fit. The sum of m and n cannot exceed length of vx.
• Stdy (optional) is a vector of standard deviations in y. Stdy must be the same length as vy.
• LBUB (optional) is a two-column matrix of lower and upper bounds on the parameters, with m + n rows.
• Acc (optional) is a convergence accuracy. The default value for Acc is 10–7.
• "noscale" (optional) is a string argument. When this argument is supplied, the input data will not be scaled to the range 0 to 1 before calculating.
If you are using more than one of the optional arguments, they must be specified in their relative order shown in the function definitions.