Functions > Data Analysis > Curve Fitting > Example: Rational Function Regression 1
Example: Rational Function Regression 1
rationalfit
Use the rationalfit function to fit a rational polynomial to data.
1. Define a data set.
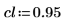
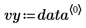
Click to copy this expression
Click to copy this expression
Click to copy this expression
This data set comes from a NIST study of semiconductor electron mobility. The predictor variable, vx, is the natural log of the density. The response variable, vy, is a measure of electron mobility.
2. Specify an order for the numerator and denominator of the rational function.
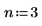
Click to copy this expression
Click to copy this expression
The fitting function has the following form:
Click to copy this expression
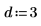
3. Define a confidence limit.
Click to copy this expression
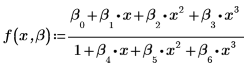
4. Call the rationalfit function.
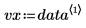
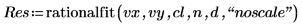
Click to copy this expression
Click to copy this expression
The first column of the output contains the values for the parameters. The second and third column contain outputs for the lower and upper confidence limits, respectively.
5. Compare the values of the parameters to the correct values, as found on the NIST web site.
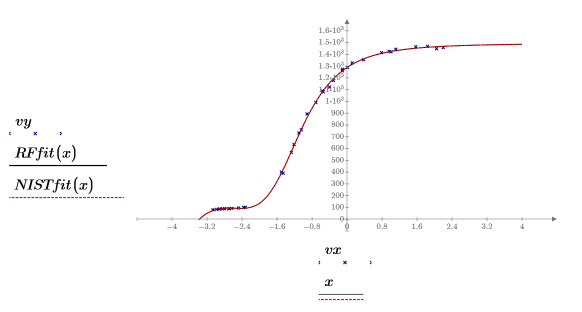
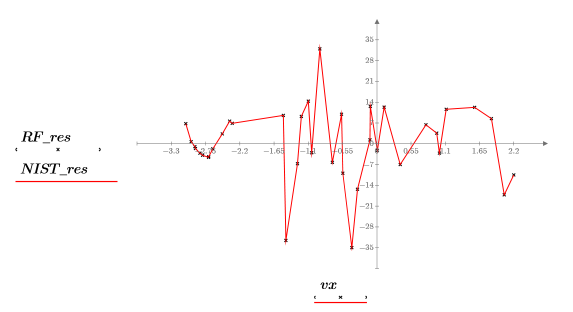
Click to copy this expression Click to copy this expression
6. Plot the data, the rational function regression, and the fit defined by the NIST parameters.
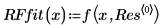
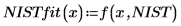
Click to copy this expression
Click to copy this expression
Click to copy this expression
The fit of the rational function regression is almost perfect, as confirmed by the correlation coefficient:
Click to copy this expression
Plot of Residuals
Create a plot of residuals to visualize the goodness of fit for the above regression.
1. Define the degree of freedom.
Click to copy this expression
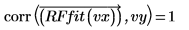
2. Calculate the residuals.
Click to copy this expression
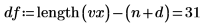
3. Calculate the residual sum of squares.
Click to copy this expression
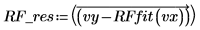
4. Calculate the standard deviation.
Click to copy this expression
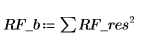
5. Repeat steps 2 to 4 with the values from the NIST website.
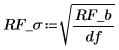
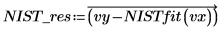
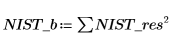
Click to copy this expression
Click to copy this expression
Click to copy this expression
6. Compare the results for the two fits.
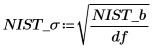
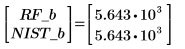
Click to copy this expression
Click to copy this expression
7. Plot the data points and the residuals.
Click to copy this expression
Constraints, Standard Deviation, and Tolerance
There are several optional arguments to rationalfit: the standard deviation vector; the lower and upper bounds matrix; the accuracy; and "no scale". You can use any of the optional arguments alone, but for the first three arguments defined above, the order of the arguments matters.
1. Create a matrix of lower and upper bounds on the parameters.
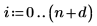
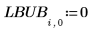
Click to copy this expression
Click to copy this expression
Click to copy this expression
2. Create a vector of standard deviations for the parameters.
Click to copy this expression
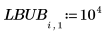
When a vector of standard deviations is entered as an argument to the rationalfit function, the solver minimizes the following function:
Click to copy this expression
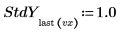
If the standard deviation is 0 for a point, then the original, undeviated function is used at that point, that is, StdYi is set to 1.
3. Set the accuracy. The default is 10-7.
Click to copy this expression
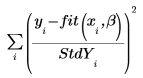
4. 4. Call the rationalfit function. Compare the returned parameter values to the correct values from the NIST web site.
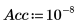
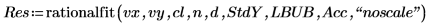
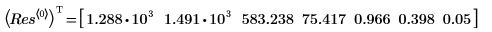
Click to copy this expression
Click to copy this expression
Click to copy this expression
The rationalfit function performs an automatic scaling on input data, so that the accuracy can remain scale-invariant. It then rescales the output parameters to match the original data. Most of the time, this ensures that your fit is achieved regardless of the relative scale of your input data. If you are having trouble achieving a good fit, add the “noscale” option string at the end of the argument list to turn off this option.
Rational Function Regression
Was this helpful?