Interpolation and Resampling
• multirate(v, n, m, [f])—Returns a version of multichannel signal v resampled by a factor of n/m, using the optional argument f as the lowpass interpolating filter.
• resample(v, m, n)—Returns a vector obtained from v by n-fold interpolation and then sampling every mth point. Input data must be real.
• upsample(v, n)—Returns an interpolated version of vector v with n times as many points as v.
Arguments
• v is a vector or matrix of real or complex numbers representing the samples of a signal. If v is a matrix, each column is processed individually.
For functions multirate and resample, if vector v contains units, then the elements of the returned vector will contain these same units.
• n is an integer, the upsampling/interpolation factor. For upsample and resample, n ≥ 2.
• m is an integer, downsampling/decimation factor. For resample, m ≥ 2.
• f (optional) is a vector of FIR lowpass filter coefficients used between upsampling and downsampling. Default filter has length 32, gain n, windowed with a Hanning taper, with cutoff frequency of:
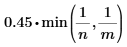
Additional Information
• The functions return the resampled signal.
• For multirate and resample, the returned vector is approximately of length n/m times the original data length.
• upsample returns an even number of points, either n times the input length or n times the input length plus 1.
• It is recommended to use multirate, because it works in the most general case and avoids the aliasing effect that might arise when downsampling a signal.
• multirate filters in the time domain, and requires only that the signal be bandlimited. upsample and resample assume periodicity of the signal, and perform operations in the frequency domain after taking an FFT.
• multirate uses the group delay of a linear-phase FIR filter to estimate where the initial output transient ends, and truncates. For filter length L, the group delay is L/2, so multirate skips the first L/2m samples of signal output. To observe the transient, zero-pad the signal. If the provided filter does not have linear-phase, some data at the beginning may be missing, so zero-padding the signal in this case is also advised.
• Filtering with multirate is carried out using a polyphase representation of the filter coefficients.