Example: Time Response of Digital Filters
Use the response and fftfilt functions to compute the output of an FIR or IIR filter by direct evaluation of the convolution. The function returns a complex vector of outputs of length n.
The technique employed by these functions is well-established and documented in most signal processing textbooks. See for example A.V. Oppenheim and R. W. Schafer, Discrete-Time Signal Processing, pp.556-558, 1989.
Lowpass IIR Filter Order
1. Define an input signal with a low-frequency and a high-frequency component.
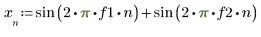
2. Compute the first 100 steps of the response of a second-order lowpass Butterworth filter with a cutoff frequency f.
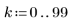
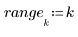
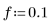
The cutoff must be from 0 to 0.5, as specified in the function description.
3. Use the iirlow function to get the transfer function coefficients.
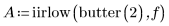
4. Use the response function to get the filter's response.
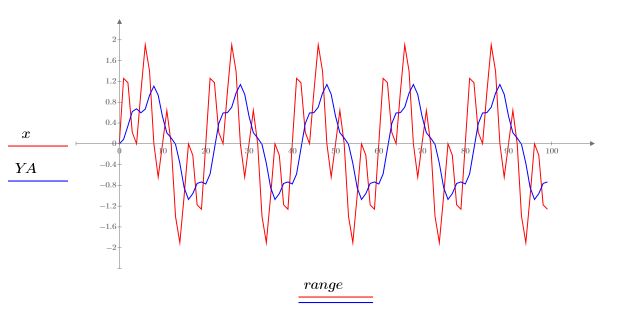
The response signal YA is smoother, has a smaller amplitude, and has a slight time shift when compared with the original signal x.
5. Specify a sixth-order lowpass Butterworth filter with the same cutoff frequency f. The response function feeds the output of the first section into the second section, and this output into the third, and so forth.
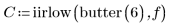
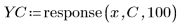
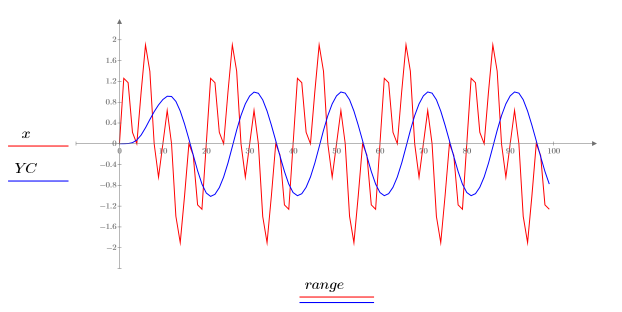
The higher order filter delivers a much smoother response, is more effective in filtering the high frequency, results in a larger time shift, and provides a sharper cutoff frequency transition.
Bandpass FIR Filter
1. Design an FIR bandpass filter F to transmit the higher of the two signal frequencies defined above.
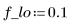
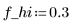
2. Compute the coefficients for a length 51 bandpass filter with passband between the above low and high frequencies, and use a Blackman taper (last argument of 6).
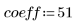
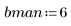
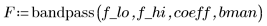
3. Calculate the delay caused by the filter.
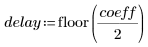
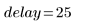
4. Apply the response function to compute the first 100 steps.
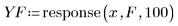
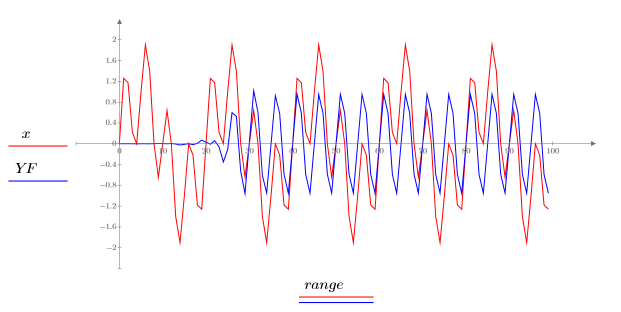
Although the filter does not transmit immediately upon initiation, it does select the high frequency (f2=0.2, T=5) very accurately.
Bandpass FIR Filter 2
Show that the following lowpass FIR filter has zero phase shift for several frequencies in its passband.
1. Define two input signals.
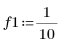
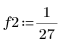
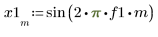
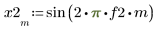
2. Define the FIR filter cutoff frequency and number of coefficients.
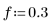
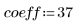
3. Compute the coefficients tapered with a Hanning window.
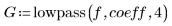
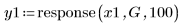
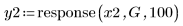
4. Calculate the delay caused by the filter.
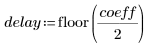
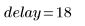
5. Define the two delayed input signals.
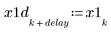
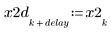
6. Plot the first delayed input signal x1d and the filter's response to x1.
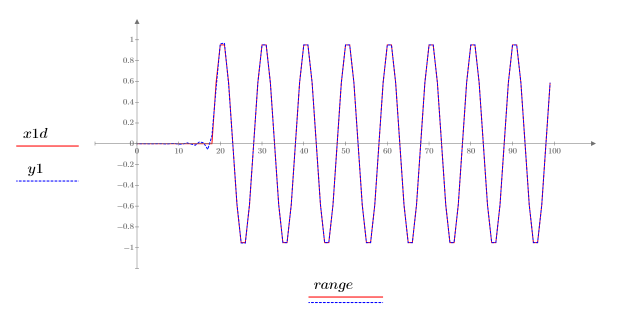
The two signals are identical and have zero phase shift.
7. Plot the second delayed input signal x2d and the filter's response to x2.
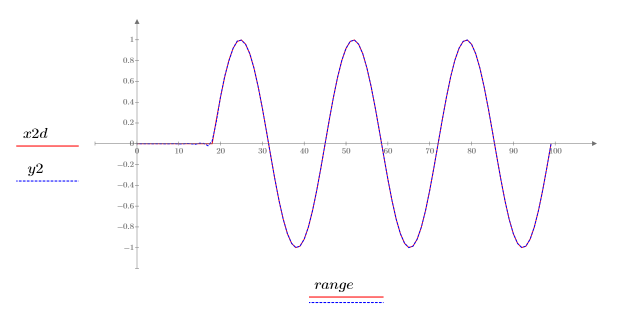
The two signals are identical and have zero phase shift.
Using response for Convolution
If the filter array has one column, the response function carries out a convolution. Thus this function provides an alternative to the FFT-based function convolve. The response is much faster for a small initial portion of the convolution of two long sequences.
1. Define a range and two arrays filled with random positive numbers from 0 to 1.
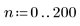
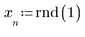
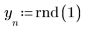
2. Apply the convolve function to the two arrays.
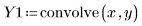
3. Use the response function to get the first 8 steps of the response.
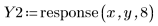
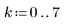
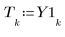


The two arrays are identical.
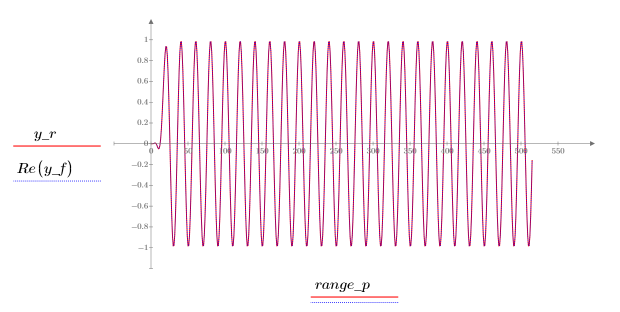
Comparing the Output of the Response and fftfilt Functions
Show that the results obtained from the response and fftfilt functions are equivalent.
1. Define a range and two frequencies.
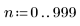
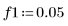
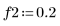
2. Define the input signal in terms of f1 and f2.
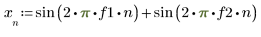
3. Create an FIR lowpass filter with a cutoff frequency f and tapered with a Hanning window.
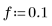
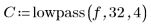
4. Calculate the filter response to the input signal.
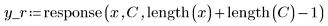
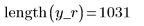
5. Apply the fftfilt function to the input signal and get the first 64 steps.
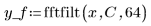
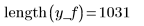
y_f is a vector of complex elements. |
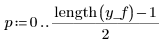
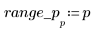
6. Plot the result of convoluting the input signal with the filter's transfer function along with the response signal. The two traces overlap completely.