Example: The Hartley Transform

Functions > Signal Processing > Additional Transforms > Example: The Hartley Transform

Use the dht function to find the Hartley transform of signals.

The defining sum for the Hartley transform is analogous to the discrete Fourier transform sum.

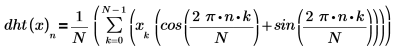
where N is the number of elements in the real data array x.

Sum of Sine Waves

Find the Hartley transform for a sum of sine waves and compare it with the magnitude of the complex Fourier transform.

1. Define the number of elements.

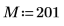
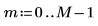
2. Use the sin function to define the input signal.

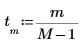
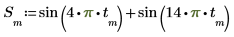
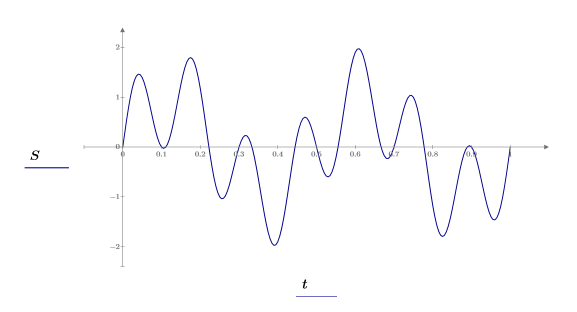
3. Plot the signal.

<region id="ID0EPDN4" actualWidth="577.15384615384619" actualHeight="312" top="537.60000000000014" left="38.400000000000006" height="312" width="577.15384615384619" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="193">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="481.153846153846" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="1">
          <axisLine position="origin" positionticmark="2" legendWidth="58.32" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="195">
              <real xmlns="http://schemas.mathsoft.com/math50">1.0</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-2" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="61.6633333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">S</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="199">
              <real xmlns="http://schemas.mathsoft.com/math50">-2</real>
            </startValue>
            <secondTickValue resultRef="201">
              <real xmlns="http://schemas.mathsoft.com/math50">-1.0</real>
            </secondTickValue>
            <endValue resultRef="203">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

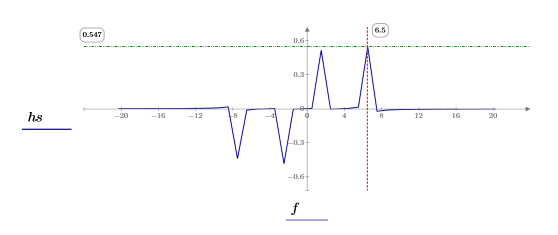
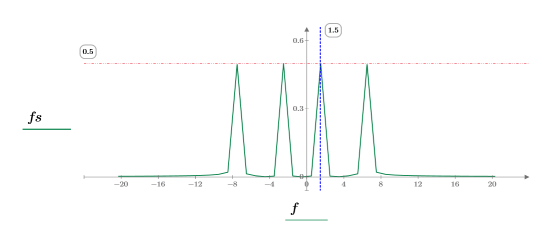
4. Use the dht function to show the discrete frequencies represented in the two sine waves, and then use the center function to shift the DC component to the center.

<region id="ID0ERGN4" actualWidth="556.61538461538464" actualHeight="312" top="1017.6000000000001" left="38.400000000000006" height="312" width="556.61538461538464" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="218">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.615384615385" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-100" end="100">
          <axisLine position="origin" positionticmark="2" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="221">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="222">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="220">
              <real xmlns="http://schemas.mathsoft.com/math50">-100</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.6" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="67.37" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="227">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">hs</id>
              </math>
              <math resultRef="228">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="224">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.6</real>
            </startValue>
            <secondTickValue resultRef="226">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

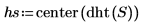
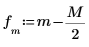
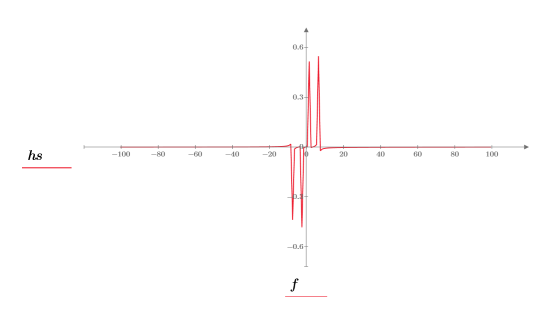
5. Use the match and max functions to find the discrete frequencies at which the peaks occur, and mark one such point with a vertical and a horizontal marker.

<region id="ID0EFJN4" actualWidth="234.18333333333334" actualHeight="36.800000000000004" top="1420.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="236">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">p1</id>
      <eval>
        <apply>
          <indexer />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">match</id>
            <sequence>
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">max</id>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">hs</id>
              </apply>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">hs</id>
            </sequence>
          </apply>
          <real>0</real>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EPKN4" actualWidth="557.95384615384614" actualHeight="235.2" top="1478.4000000000003" left="38.400000000000006" height="235.2" width="557.95384615384614" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="242">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="461.953846153846" height="177.6" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-20" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="243" display="true" color="#FFFF0000" line-style="Dash" value="6.5">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">f</id>
                <id xml:space="preserve">p1</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="249">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="250">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="246">
              <real xmlns="http://schemas.mathsoft.com/math50">-20</real>
            </startValue>
            <endValue resultRef="248">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.6" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="67.37" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="251" display="true" color="#FF008000" line-style="DashDotDot" value="0.547390503599252">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">hs</id>
                <id xml:space="preserve">p1</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="259">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">hs</id>
              </math>
              <math resultRef="260">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="254">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.6</real>
            </startValue>
            <secondTickValue resultRef="256">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </secondTickValue>
            <endValue resultRef="258">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

6. Use the dft and center functions to get and center the discrete Fourier Transform.

<region id="ID0ESMN4" actualWidth="157.48666666666668" actualHeight="47.2" top="1785.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="272">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="*">dfts</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">center</id>
        <apply>
          <div />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dft</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          </apply>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">M</id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

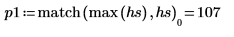
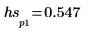
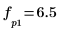
7. Plot the absolute values of the DFT.

<region id="ID0EQON4" actualWidth="556.61538461538464" actualHeight="312" top="1881.6000000000004" left="38.400000000000006" height="312" width="556.61538461538464" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="276">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.615384615385" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-100" end="100">
          <axisLine position="origin" positionticmark="0" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="279">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="280">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="278">
              <real xmlns="http://schemas.mathsoft.com/math50">-100</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="65.9166666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="287">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">fs</id>
              </math>
              <math resultRef="288">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="282">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="284">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </secondTickValue>
            <endValue resultRef="286">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

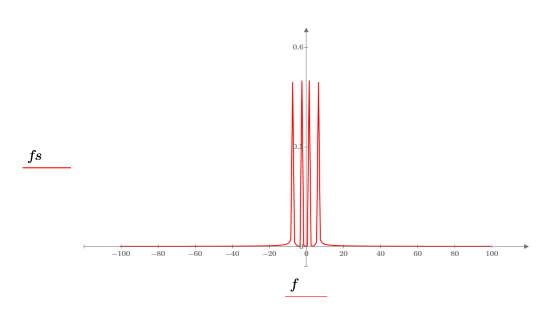
8. Use the match and max functions to find the discrete frequencies at which the peaks occur.

<region id="ID0EIQN4" actualWidth="231.2766666666667" actualHeight="36.800000000000004" top="2265.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="297">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">p2</id>
      <eval>
        <apply>
          <indexer />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">match</id>
            <sequence>
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">max</id>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">fs</id>
              </apply>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">fs</id>
            </sequence>
          </apply>
          <real>1</real>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ESRN4" actualWidth="556.95384615384614" actualHeight="235.20000000000002" top="2323.2000000000003" left="38.400000000000006" height="235.20000000000002" width="556.95384615384614" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="303">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.953846153846" height="177.6" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-20" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="304" display="true" color="#FF0000FF" line-style="Dash" value="1.5">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">f</id>
                <id xml:space="preserve">p2</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="310">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="311">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="307">
              <real xmlns="http://schemas.mathsoft.com/math50">-20</real>
            </startValue>
            <endValue resultRef="309">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="65.9166666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="312" display="true" color="#FFED1D2F" line-style="DashDotDot" value="0.50020306790574232">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">fs</id>
                <id xml:space="preserve">p2</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="320">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">fs</id>
              </math>
              <math resultRef="321">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="315">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="317">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </secondTickValue>
            <endValue resultRef="319">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

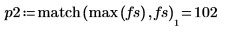
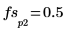
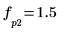
The close relationship between the Hartley transform and the Fourier transform can be demonstrated by showing how to compute phase and magnitude from the Hartley transform. This can be done using a small data set.

Short and Noisy Signal

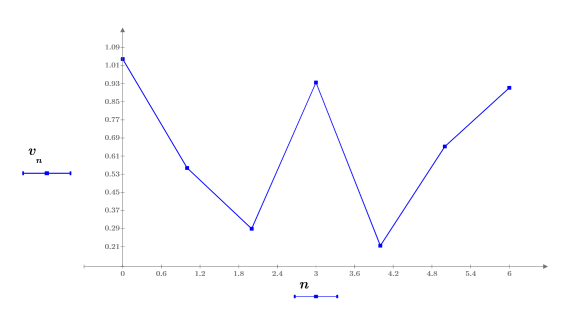
1. Define and plot a noisy input signal of 7 sample points.

<region id="ID0E4UN4" actualWidth="575.84615384615381" actualHeight="312" top="2860.8000000000006" left="38.400000000000006" height="312" width="575.84615384615381" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="339">
          <traceStyle color="#FF0000FF" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="479.846153846154" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="6">
          <axisLine position="bottom" positionticmark="-1" legendWidth="61.7533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="340">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">n</id>
              </math>
              <math resultRef="341">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.21" end="1.09">
          <axisLine position="origin" positionticmark="0" legendWidth="66.5833333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="342">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">v</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </math>
              <math resultRef="343">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

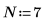
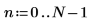
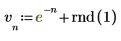
2. Compute and center the discrete Hartley transform.

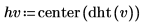
3. Compute the odd and even parts of the discrete Hartley transform (these formulas assume an odd value of N).

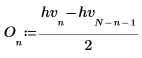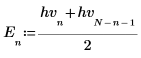4. Use the angle function to calculate the phase vector.

<region id="ID0EK2N4" actualWidth="145.02333333333334" actualHeight="36.800000000000004" top="3475.2000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="354">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id xml:space="preserve" labels="*">ϕ</id>
        <id xml:space="preserve" labels="*">n</id>
      </apply>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">angle</id>
        <sequence>
          <apply>
            <indexer />
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">E</id>
            <id xml:space="preserve">n</id>
          </apply>
          <apply>
            <neg />
            <apply>
              <indexer />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">O</id>
              <id xml:space="preserve">n</id>
            </apply>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

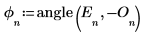
5. Define the magnitude vector.

6. Use the phase, phasecor, and center functions to create the phase vector.

<region id="ID0EH6N4" actualWidth="282.13333333333333" actualHeight="25.6" top="3648.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="358">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="*">phs2</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phasecor</id>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phase</id>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">center</id>
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dft</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">v</id>
            </apply>
          </apply>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

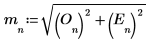
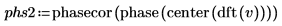
7. Use the augment function to compare the phase results to that obtained via the Fourier transform.

<region id="ID0EJBO4" actualWidth="353.5533333333334" actualHeight="137.2" top="3801.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="360">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">augment</id>
        <sequence>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phasecor</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ϕ</id>
          </apply>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">phs2</id>
        </sequence>
      </apply>
      <unitOverride>
        <id xml:space="preserve" labels="*">π</id>
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

The phase results agree.

8. Use the dft and center functions to create the magnitude vector.

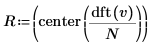
9. Use the augment function to compare the magnitude results to that obtained via the Fourier transform.

<region id="ID0EZEO4" actualWidth="244.03333333333336" actualHeight="137.2" top="4147.2000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="364">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">augment</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
          <apply>
            <vectorize />
            <apply>
              <absval />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">R</id>
            </apply>
          </apply>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

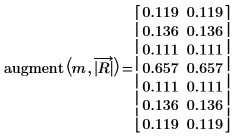
The magnitude results agree.

For a thorough treatment of the Hartley transform and its applications, see Ronald Bracewell, The Hartley Transform (Oxford University Press).