Example: Solving a First-Order ODE Initial Value Problem
Solve an ordinary differential equation of the form:
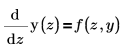
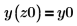
1. Enter the initial value problem specifics.
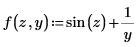
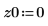
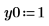
2. Enter the desired solution parameters - Endpoint of solution interval, then number of solution values on [t0, t1].
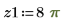
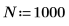
Odesolve
Use a solve block and the odesolve function to solve the differential equation.
1. Define the derivative of y inside a solve block.

2. Plot y versus z.
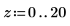
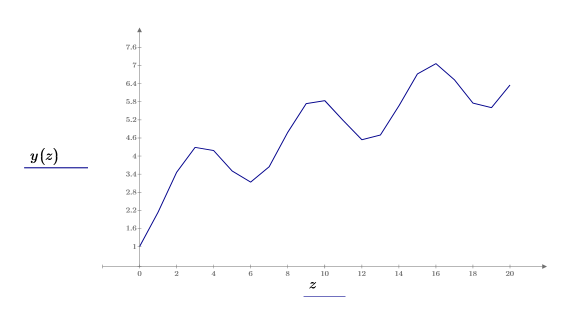
3. Use the odesolve solution parametrically within the solve block.

The output, fy(k), is a function of a function, so you must specify the value of the parameter for which you would like the solution function.
4. Assign the result to an ordinary function name without the independent variable t.
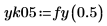
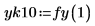
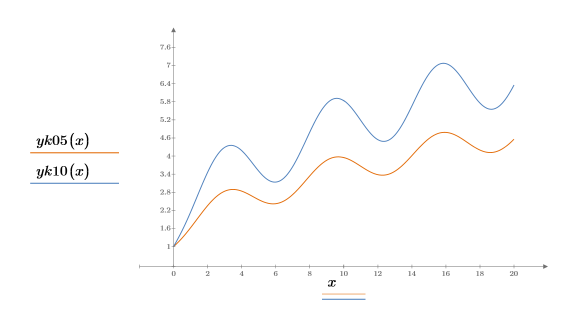
5. Plot the two curves.
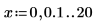
Adams, rkfixed, Rkadapt, Bulstoer, and Radau
Another way to solve the differential equation is by using the ODE solver Adams.
1. Define solver parameters - vector of initial solution values, and the derivative function.
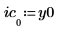
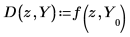
The second argument of the derivative function must be a vector of unknown function values.
2. Evaluate the Adams matrix.
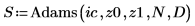
3. Plot the solution function values Y versus the independent variable values T.
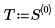
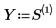
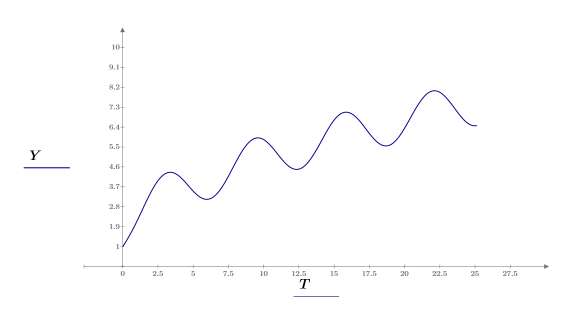
The results of odesolve are just an interpolated version of the results from the single-line function solvers. The Solve Block version allows more natural notation for the problem, while the function returned by odesolve is the interpolation of the same table that is returned by the single-line solver.