Example: Modified Bessel Functions of the Second Kind
Show the relationship between functions K0, K1, and Kn. Also show the relationships between these functions and their scaled versions.
1. Define two step range variables:
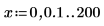
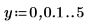
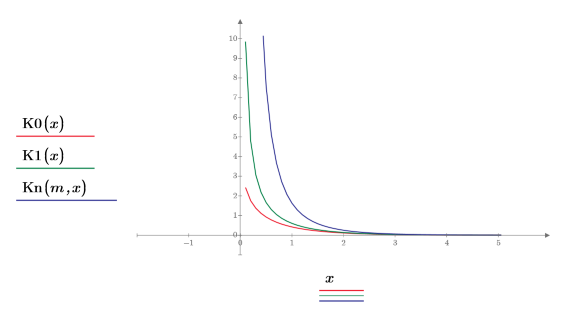
2. Plot functions K0 and K1. Add the second order function Kn to the plot:
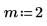
3. Plot the fifth and eighth order function Kn:
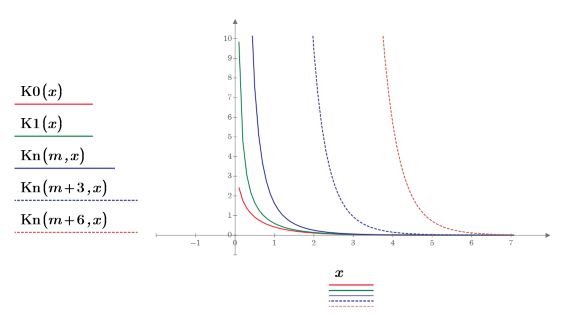
• The higher the order of the Kn function, the larger the shift of the function to the right. • All orders of the Kn function approach infinity at x=0. |
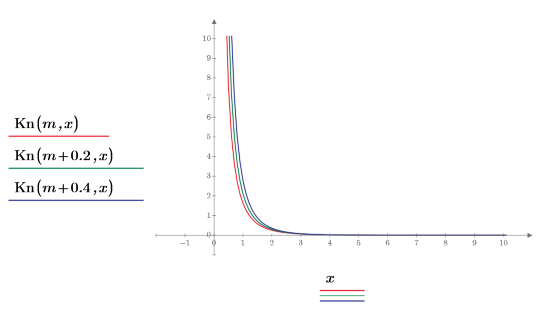
4. Plot function Kn with small difference in m to show that they approach infinity at the same rate:
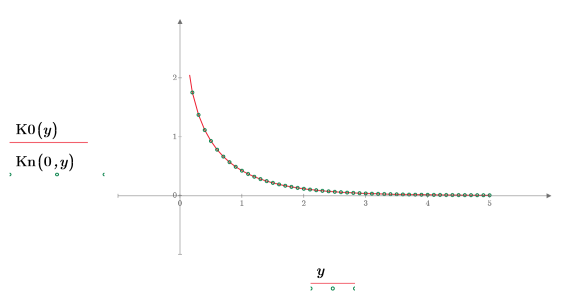
5. Create a plot to show that K0(y)=Kn(0,y). Reset the tick mark values to zoom in the x-axis in order to show more details:
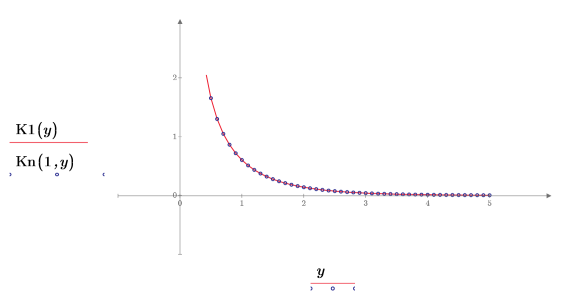
6. Create a plot to show that K1(y)=Kn(1,y). Reset the tick mark values to zoom in the x-axis in order to show more details:
7. Use symbolic evaluation to show the relationship between each function and its scaled version:
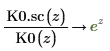
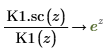
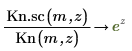
8. Create a plot to show that:
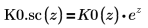
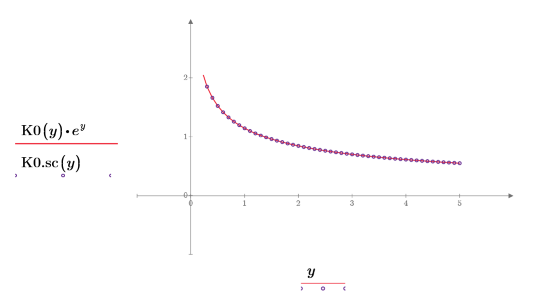
The modified Bessel functions of the second kind have no peaks.