Functions > Special Functions > Bessel Functions > Example: Kelvin Functions
Example: Kelvin Functions
Show the relationship between functions ber and bei. These functions have no scaled versions.
1. Plot the zeroth order functions ber and bei:
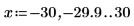
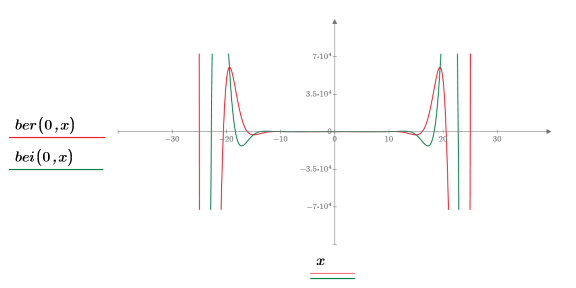
Click to copy this expression
Click to copy this expression
The two functions appear symmetrical.
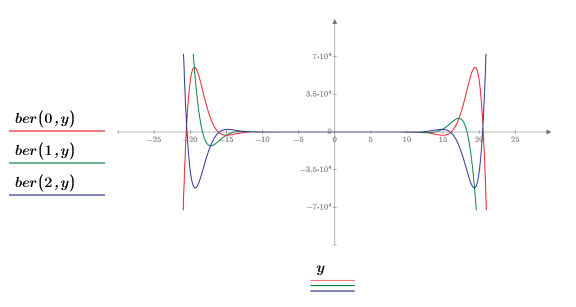
2. Reset the tick mark values to zoom in the x-axis in order to show how the two peaks of the ber and bei functions change as the order is increased:
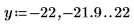
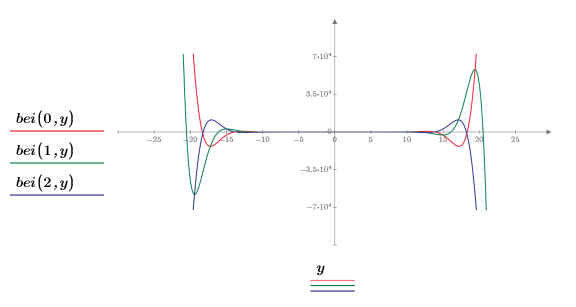
Click to copy this expression
Click to copy this expression
Click to copy this expression
3. Use symbolic evaluation to show the relationships between the ber and bei functions with function Jn, and then create plots to show the results visually.
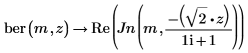
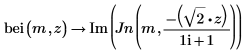
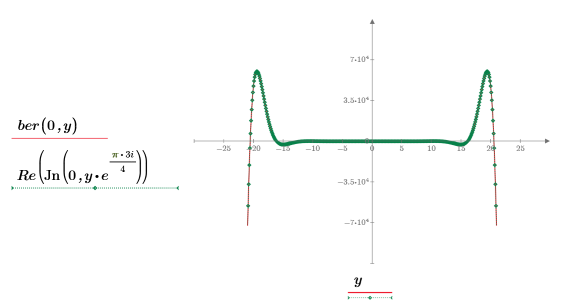
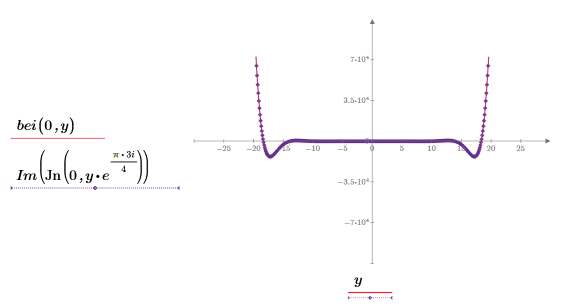
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
This example focuses on the ber function, but the same observations apply to function bei.
4. Define vector Z1 using function ber:
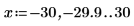
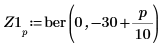
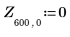
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
* 
Functions localmin and localmax require an input matrix of two columns. Pass vector Z to function augment to create such a matrix.
Click to copy this expression
5. Find the local minimas of function ber:
Click to copy this expression
The ber function has 8 minimas when m=0. The function is symmetric. Higher order functions have different number of minimas with different locations and amplitudes.
6. Find the local maximas of function ber:
Click to copy this expression
The ber function has 7 peaks when m=0. The function is symmetric. Higher order functions have different number of maximas with different locations and amplitudes.
7. Find the vertical coordinates of the four right-hand side minimas.
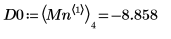
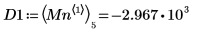
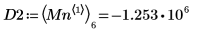
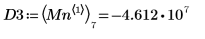
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
8. Use function match to find the index of each matching minima then find the equivalent horizontal coordinates.
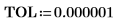
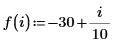
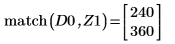
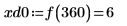
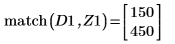
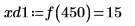
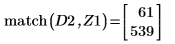
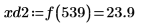
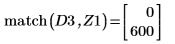
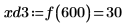
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
9. Find the vertical coordinates of the four right-hand side maximas.
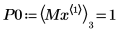
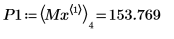
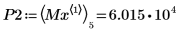
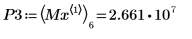
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
10. Use function match to find the index of each matching maxima then find the equivalent horizontal coordinates.
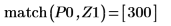
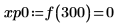
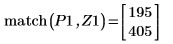
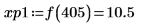
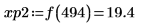
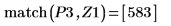
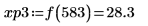
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
* 
The range of maxima and minima amplitudes varies greatly and makes it hard to see all of them on one plot.
11. Use markers to show the first minima (D0) and first maxima (P0):
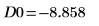
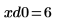
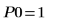
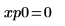
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
As expected, the graph shows a second minima to the left of the y-axis.
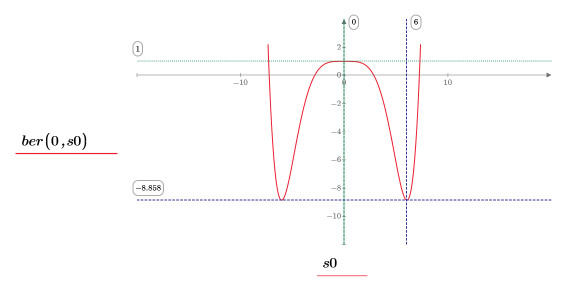
12. Use markers to show the next minima (D1) and next maxima (P1):
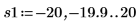
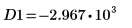
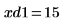
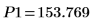
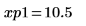
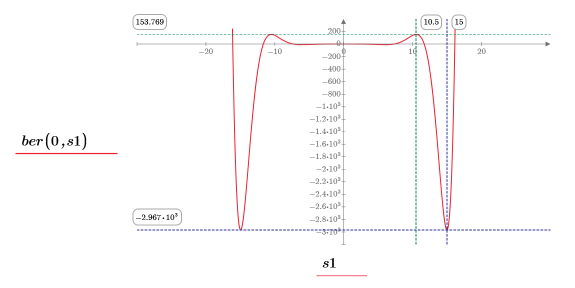
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
As expected, the graph shows a second minima and a second maxima to the left of the y-axis.
13. Use markers to show the next minima (D2) and next maxima (P2):
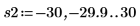
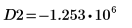
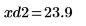
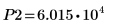
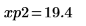
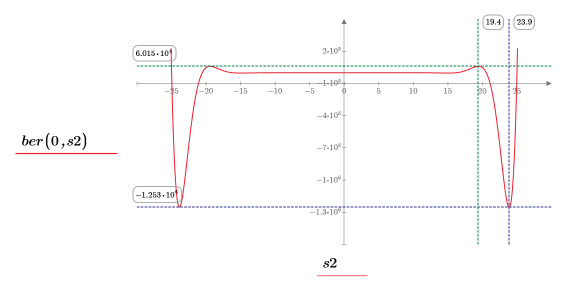
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
As expected, the graph shows a second minima and a second maxima to the left of the y-axis.
14. Use markers to show the next minima (D3) and next maxima (P3):
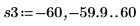
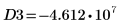
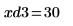
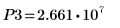
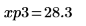
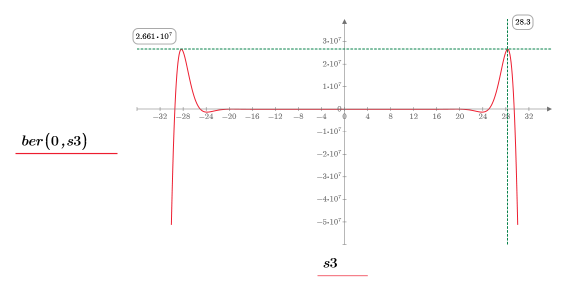
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
As expected, the graph shows a second maxima to the left of the y-axis.
* 
Minima (D3), and its left-side equivalent, fall exactly on the edges of the range, so it is better to ignore them.
Bessel Kelvin Functions
Was this helpful?