Example: FIR Filters by Remez Exchange
The remez function implements the Remez exchange algorithm for FIR filter design.
See Theory and Application of Digital Signal Processing by Rabiner and Gold (Prentice-Hall, Inc.) and Digital Filter Design by Parks and Burrus (Wiley-Interscience) for a discussion of the algorithm and examples.
Lowpass Filter
1. Define a response of 1 in the passband and 0 in the stopband, and interpolate a straight-line transition between the passband and stopband edges.
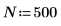
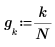
In general, the number of points in the frequency grid should be on the order of 8 to 10 times the filter length, with frequencies starting at 0 and increasing uniformly to just under 0.5. Definition of the response requires definition of the band edges and the weights assigned to the errors in each band. The algorithm minimizes the maximum weighted error over the frequency range [0, 0.5].
2. Define the passband and stopband edges:
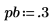
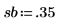
3. Define the passband, stopband and transition band weights:
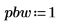
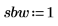
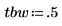
4. Define a function that gives the desired response as a function of frequency. Evaluating at each grid point builds the response vector.
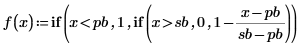
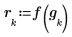
5. Define the weight vector which assigns to each grid point the weight for the corresponding band.
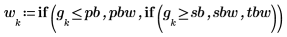
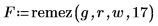
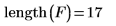
7. Use function gain to calculate, for this odd-length filter, the maximum passband and stopband errors which are given by the gain at 0 and at .5:
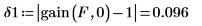
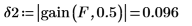
8. Plot the function and its frequency response from 0 to .5.
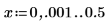
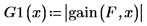
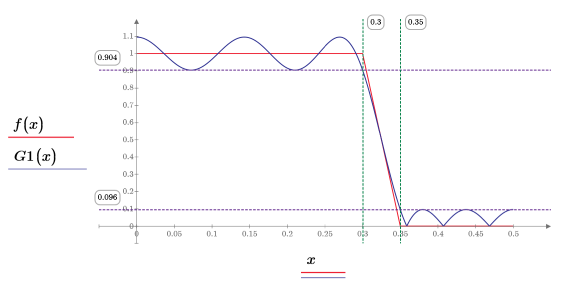
The ten extremal frequencies are visible, including the point where the (1 - δ1) line crosses the passband edge pb and the point where the δ2 line crosses the stopband edge sb. The error alternates uniformly on the extremal frequencies in each band. To see an example in which the two errors d are unequal, change the stopband weight to .5 in the filter spec above.
Bandpass Filter
1. Define a response function which is constructed by adding functions for the response in each transition band and in the passband.
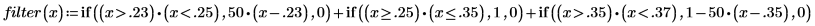
2. Apply the filter function to the whole grid at once using the vectorize operator. The weights are uniform.
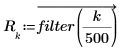
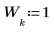
3. Generate a filter with 45 coefficients:
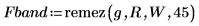
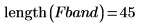
4. Plot the frequency response of the filter: