Example: Elementwise Phase
Functions phase and phasecor return, respectively, phase angles and phase angles corrected for jump discontinuities.
Function phasecor takes a real vector representing phase information as argument then walks through the vector adding multiples of 2p (maintaining the integrity of the data) when necessary to produce a continuous data set.
Four-Element Vector
1. Define a simple complex vector.
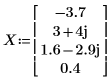
2. Use the phase function to find the element-wise phases.
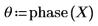
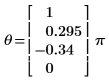
Typically phase computations are done elementwise without regard to past phase history. This results in large jump discontinuities in the resulting phase data due to the change in angle from +p to -p when you cross the negative real axis.
3. Define another complex vector.
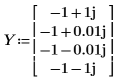
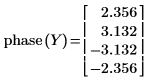
The resulting phases show a large jump discontinuity between the second and third element.
4. Apply the phasecor function to eliminates these jump discontinuities.
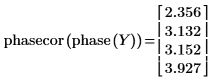
Noisy Signal
1. Define the signal parameters.
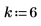
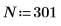
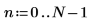
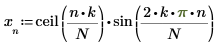
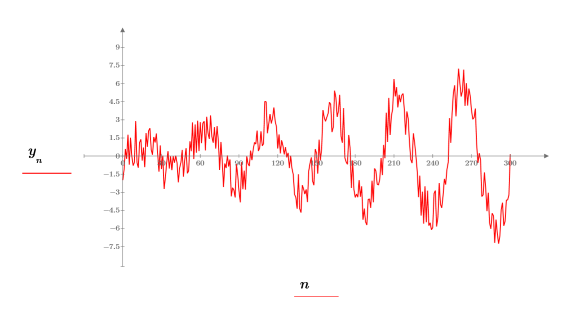
3. 3. Use the whiten function to add white noise and then plot the resulting signal.
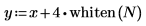
4. Use the dft function to calculate the Fourier Transform of the sample signal.
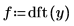
5. Apply the phase function to the Fourier Transform of the sample signal.
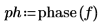
6. Plot the phase signal.
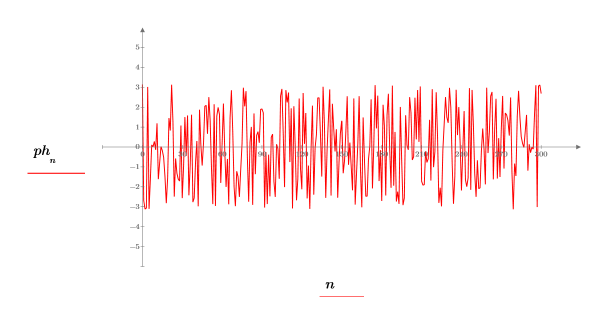
7. Use the phasecor function to correct the phase into a continuous signal, and then plot the resulting output.
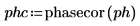
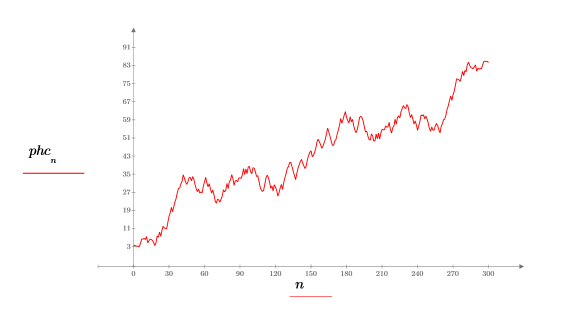
The phasecor function can be fooled if the phase changes too rapidly.
8. Set the value of the fractional frequency f0 then plot the output of phase and phasecor.
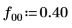
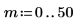
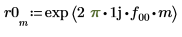
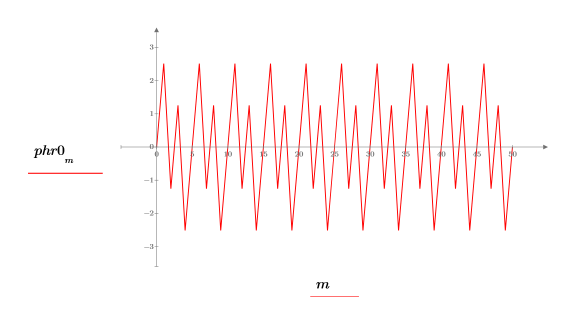
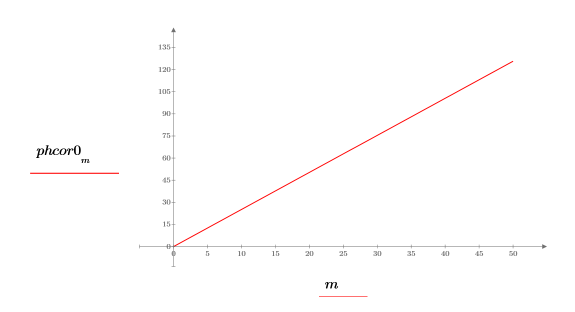
9. Calculate the outputs of phase and phasecor for fractional frequency f0 values of 0.45, 0.50 and 0.55.
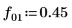 | 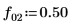 | 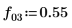 |
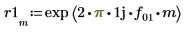 | 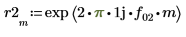 | 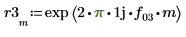 |
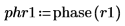 | 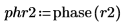 | 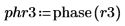 |
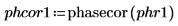 | 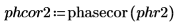 | 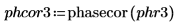 |
10. Plot the outputs of the phase function on a single plot.
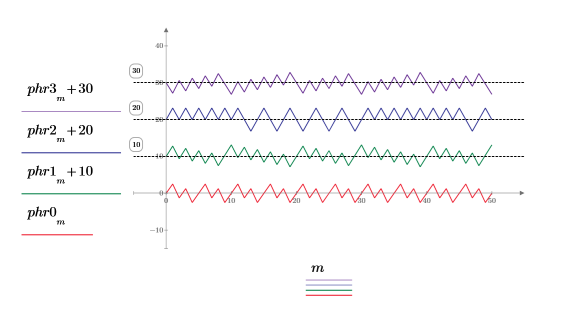
The traces are artificially shifted in the y-axis direction in order to show the phase trace for each frequency.
11. Plot the outputs of the phasecor function on a single plot.
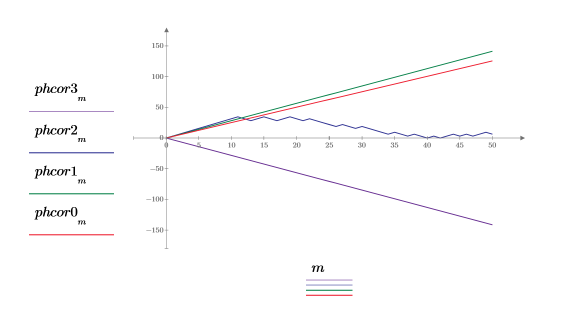
The output of phasecor increases its slope in the positive direction as fractional frequency increases from 0.40 to 0.45 to 0.50, and then it becomes negative when the fractional frequency is set to 0.55. See the previous phase plot.