Example: Chi-Square Test for Goodness of Fit
Perform a chi-square test to determine the goodness of fit between observed and expected results.
1. Define the vectors of the observed and expected frequencies.
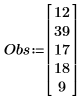 |
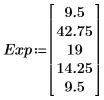 |
The expected frequencies must be greater than or equal to 5 for this analysis to be valid. The sum of the observed values must be equal to the sum of the expected values:
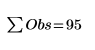 |
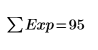 |
2. Use the length function to calculate the number of degrees of freedom, and the chi-square statistic.
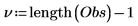 |
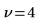 |
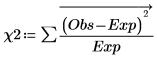 |
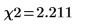 |
3. Define the significance level.
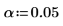
4. State the null and the alternative hypothesis.
H0 : The expected results do fit the observations.
H1 : The expected results do not fit the observations.
5. Use the pchisq function to calculate the p-value and test the hypothesis. In this example, all of the Boolean expressions evaluate to 1 when the null hypothesis is true (you do not reject H0).
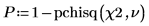
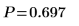
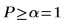
There is a 0.697 probability that the test statistic is greater than the one observed, assuming that the null hypothesis is true. The comparison between the p-value and the significance level indicates there is no evidence that the alternative hypothesis is true.
6. Use the qchisq function to calculate the limit of the critical region and test the hypothesis.
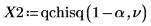
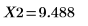
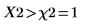
Accept the null hypothesis. There is evidence that the expected results fit the observations.
7. Plot the chi-squared probability distribution function dchisq, then use vertical markers to mark the chi-squared statistic and the limit of the critical region.
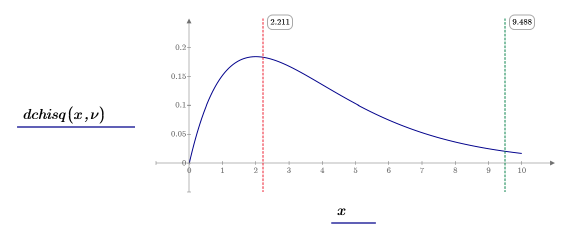
8. Use the rchisq function to create a vector of 9 random numbers having the chi-squared distribution and 3 degrees of freedom:

Recalculating the worksheet causes function rchisq to return a new set of random numbers.