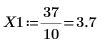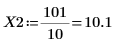Example: Bessel Functions of the Second Kind
Show the relationship between functions Y0, Y1, and Yn. Also show the relationships between these functions and their scaled versions.
1. Define two step range variables:
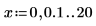
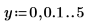
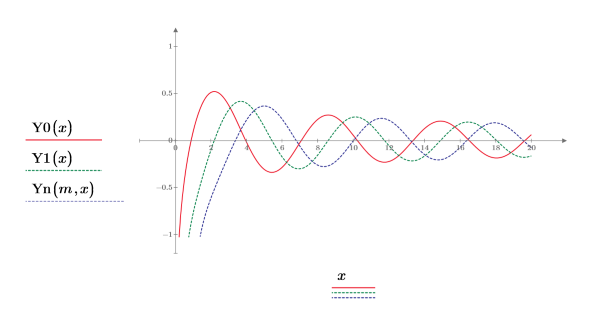
2. Plot functions Y0 and Y1. Add the second order function Yn to the plot:
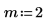
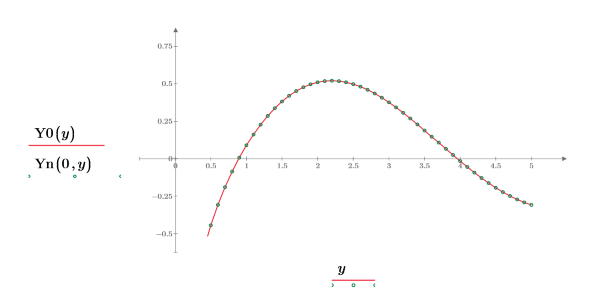
3. Create a plot to show that Y0(y)=Yn(0,y). Reset the tick mark values to zoom in the x-axis in order to show more details:
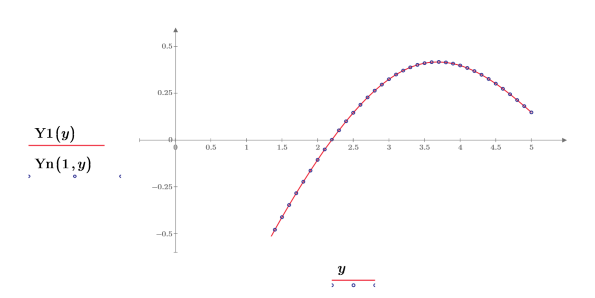
4. Create a plot to show that Y1(y)=Yn(1,y). Reset the tick mark values to zoom in the x-axis in order to show more details:
5. Use symbolic evaluation to show the relationship between each Bessel function of the second kind and its scaled version:
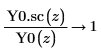
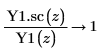
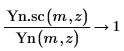
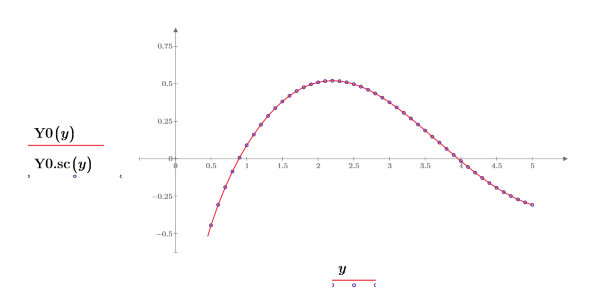
6. Create a plot to show that:
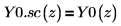
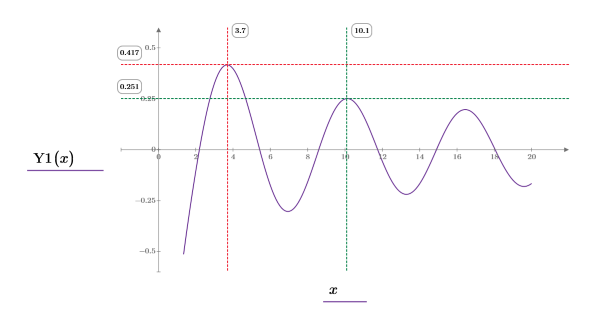
7. Calculate the coordinates of the first two peaks of Y1. Use functions augment and localmax to identify the peaks that fall within the specified range:
Bessel functions of the second kind are not defined at 0.
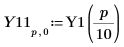
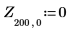
Function localmax requires an input matrix of two columns. Function augment is used to create such a matrix.
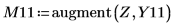
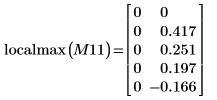
Since the function is not defined at 0, you can ignore the first local maxima at (0, 0).
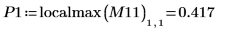
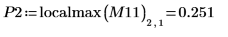
8. Use function match to find the horizontal values where the peaks occur. Reduce the value of TOL to get the most accurate results:
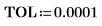
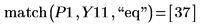
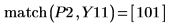
9. Add markers to the plot to mark the first two peaks:
The step range variable has a step of 0.1. This means that the peaks occur at 1/10 the element index identified by function match or 3.7 and 10.1 respectively.