Example: Airy Functions
Show the relationship between functions Ai, Bi, DAi and DBi. Also show the relationships between these functions and their scaled versions.
1. Use symbolic evaluation to show that function DAi is the first derivative of function Ai, and that function DBi is the first derivative of function Bi:
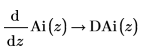
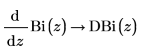
2. Define a horizontal step range variable and then plot functions Ai and Bi:
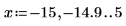
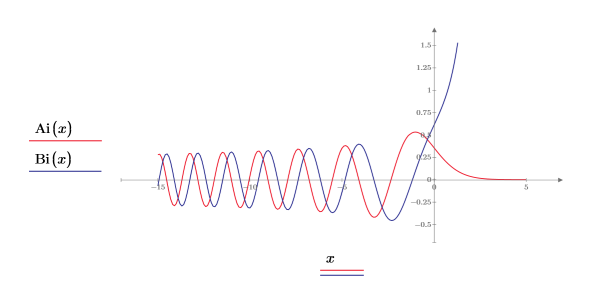
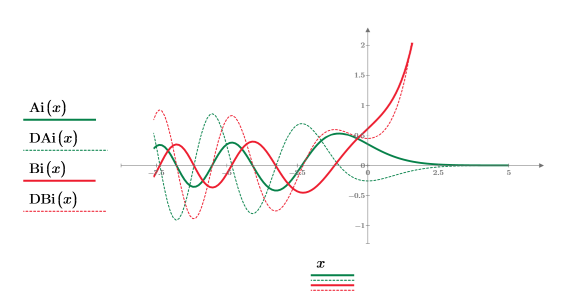
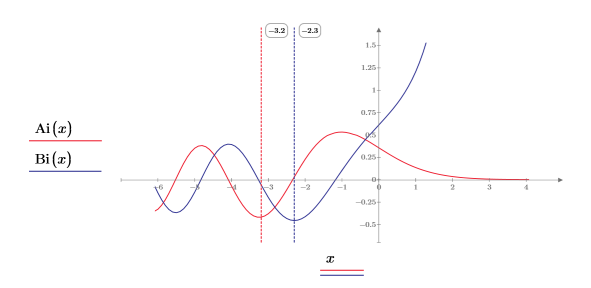
The two functions look similar, but differ in phase, along the x-axis until they begin to diverge as -x approaches zero.
3. Define vectors Z1 and Z2 using Ai and Bi:
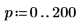
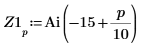
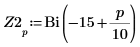
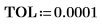
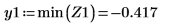
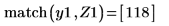
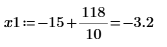
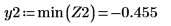
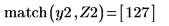
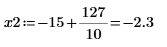
5. Add vertical markers to show the last minimas before the functions begin to diverge:
6. Use symbolic evaluation to show the relationship between each function and its scaled version:
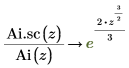
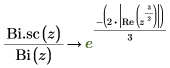
7. Create a plot to show that:
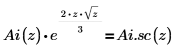
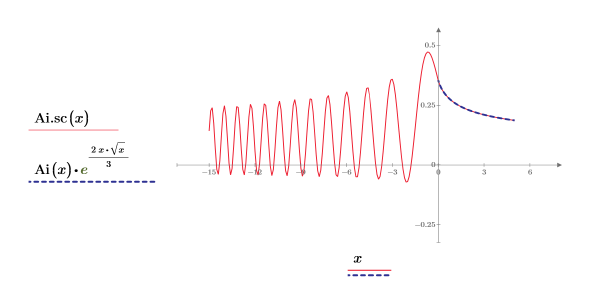
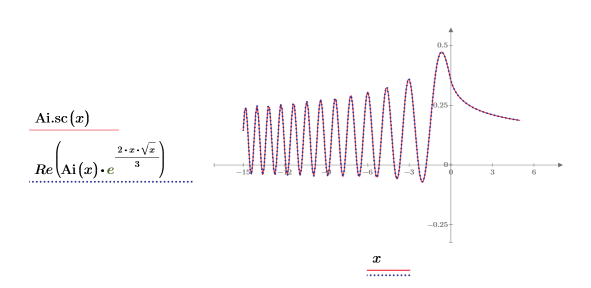
The second trace has complex values for negative values of x.
8. Recreate the previous plot to show the real values of the second trace:
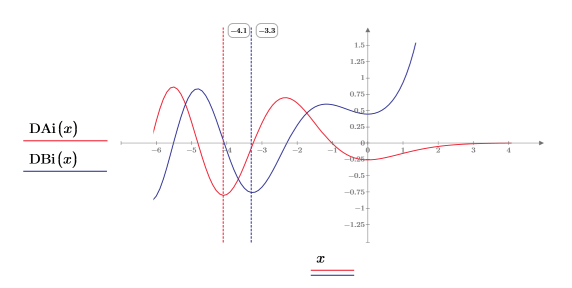
9. Plot functions DAi and DBi:
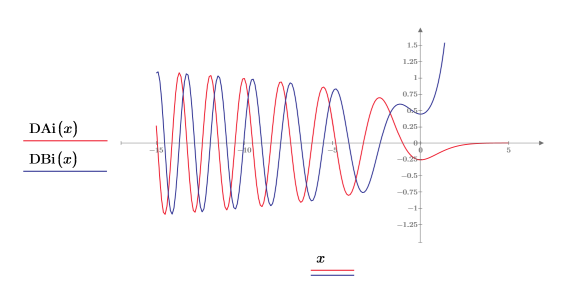
The two functions look similar, but differ in phase, along the x-axis until they begin to diverge as -x approaches zero.
10. Save DAi and DBi into vectors Z11 and Z21 respectively:
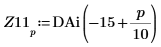
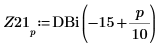
11. Find the coordinates of the local minimas of DAi and DBi that are closest to zero.
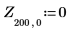
Function localmin requires an input matrix of two columns. Vector Z is used by function augment to create such a matrix.
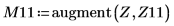
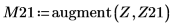

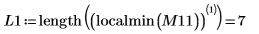
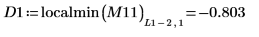

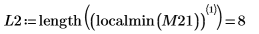
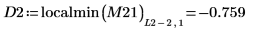
12. Find the matching coordinates of the minimas of DAi and DBi:
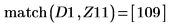
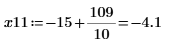
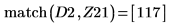
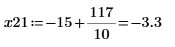
13. Add vertical markers to show the last minimas before the functions begin to diverge:
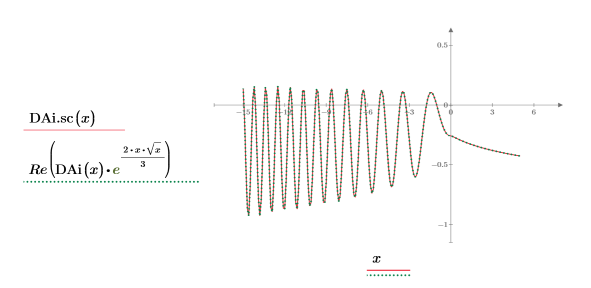
14. Use symbolic evaluation to show the relationship between each function and its scaled version:
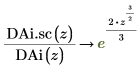
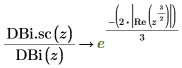
15. Create a plot to show that:
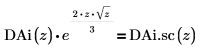
16. Compare functions Ai, DAi, Bi and DBi by plotting them on the same graph: