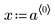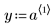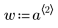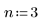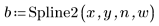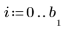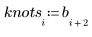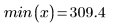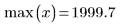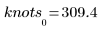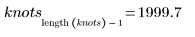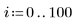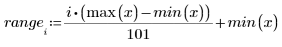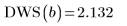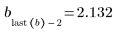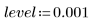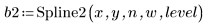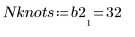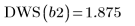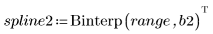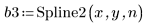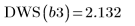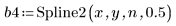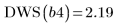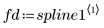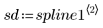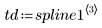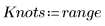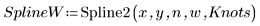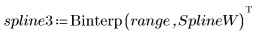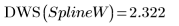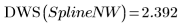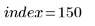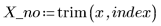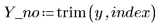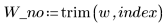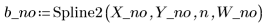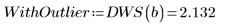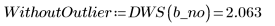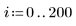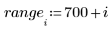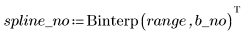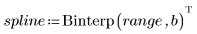範例:最小平方雲規線
Spline2、Binterp 與 DWS
使用
Spline2 函數求解
Binterp 所需的最佳節集合,以計算最小平方雲規線內插。
1. 定義數據集。
w 是在 y 中提供預估隨機誤差之標準差的加權向量。
2. 定義所要之雲規線多項式的角度。
3. 呼叫 Spline2 函數。
向量 b 的第一個元素是 B 雲規線階數。第二個元素提供區間 (knots - 1) 值。接下來的元素皆為節值。其餘的元素包含用於 B 雲規線基底函數的係數。
自動產生的第一個及最後一個節,與原始 x 數據的端點相符:
4. 呼叫 Binterp 函數取得符合 x 範圍的值域。
列 i / spline1 包含內插值,以及值域 i 中所定義點上的一階、二階及三階導數。
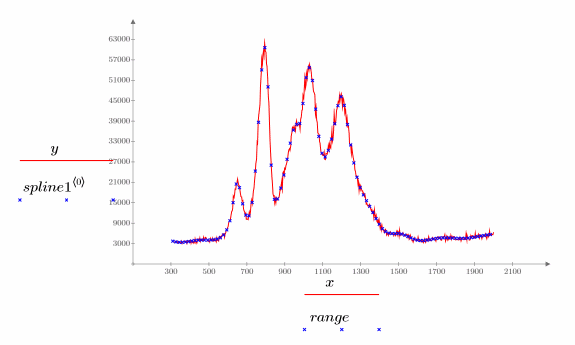
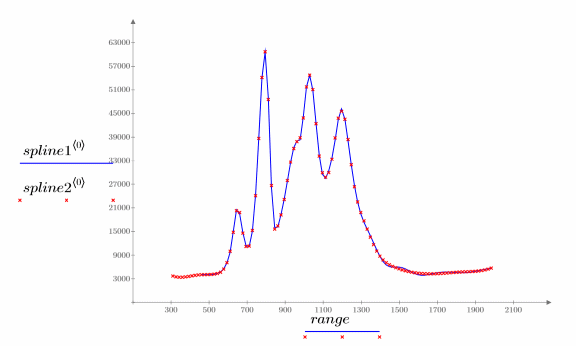
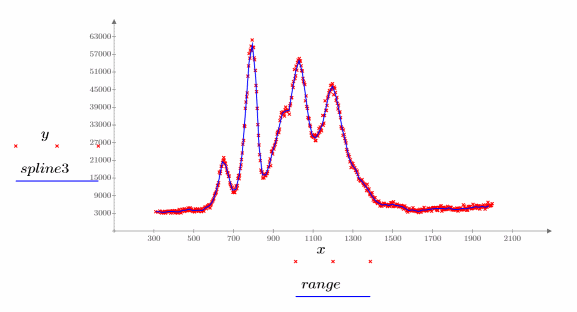
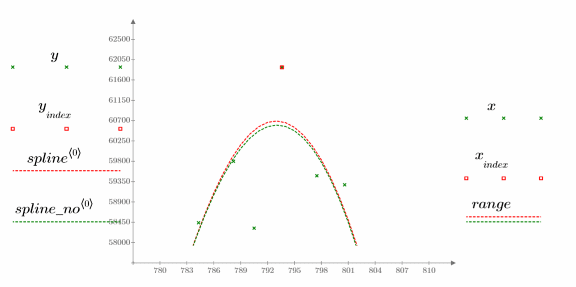
5. 繪製原始數據與內插的雲規線。
最佳節數及間距由 Durbin-Watson 統計決定。此統計應約為 2 才會出現好的擬合。使用
DWS 函數或從矩陣
b 萃取相關元素,即可求得統計:
6. 使用 Spline2 的最後一個選用引數 (0 至 1 的百分比),為 Durbin-Watson 檢驗提供顯著程度或拒絕程度。
雖然並非一律如此,但一般而言,拒絕程度愈高,產生的節愈多,計算也愈長。
7. 計算 Spline2 所用的節數。
8. 呼叫 DWS 函數計算 Durbin-Watson 統計。
9. 繪製這兩條內插的雲規線。
無需權重即可進行內插:
內插可無需權重,但需要有拒絕程度:
雲規線導數
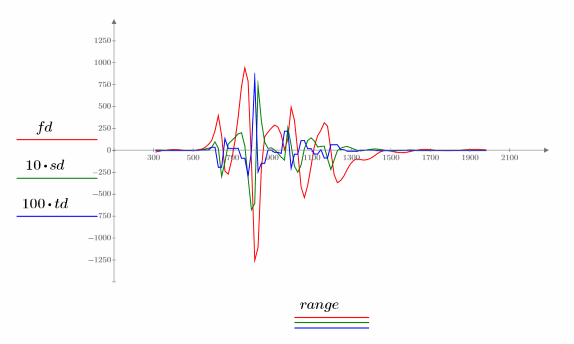
繪製內插雲規線的前三個導數。
提供您本身的節
您可為雲規線內插提供自己的節。
1. 定義節字串。
2. 繪製內插的雲規線。
您可提供無加權向量的節:
離群值
您可查看移除雲規線內插離群值的效果。
在第二個數據高峰的最高點出現可疑的點。
2. 從數據集及加權函數中移除點。
3. 呼叫 Spline2 函數取得新的數據集。
根據 Durbin-Watson 統計,擬合已改善:
4. 比較可疑數據值上的內插結果:
移除離群值後,雲規線會略微下降。