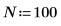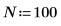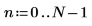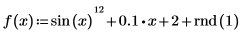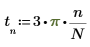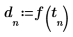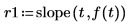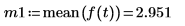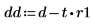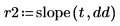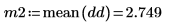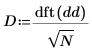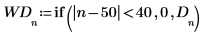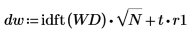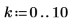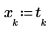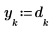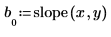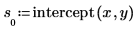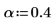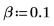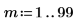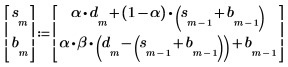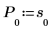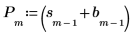예제: 필터링과 지수 평활 비교
Detrending and Lowpass Filtering in the Transform Domain 방법과 Time-domain Iterative Exponential Smoothing 방법을 사용하여 얻은 평활 결과를 비교합니다.
1. 데이터 점 수를 정의합니다.
2.
sin 및
rnd 함수를 사용하여 평활화할 함수를 정의합니다.
3. 각 표본의 시간을 나타내는 벡터를 생성합니다.
4.
slope 함수를 사용하여 신호에 가장 적합한 선의 기울기를 얻은 다음
mean 함수를 사용하여 신호의 평균을 얻습니다.
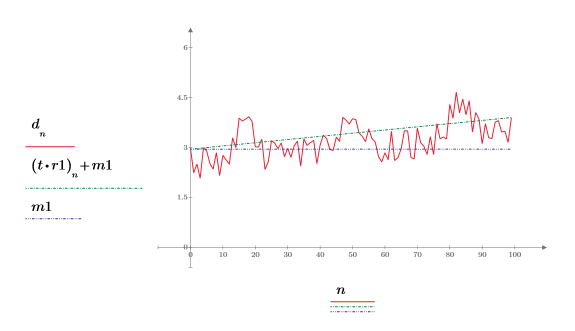
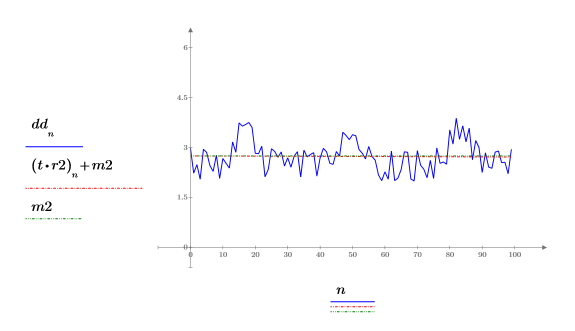
5. 함수를 도표화하고 추세선과 평균선을 표시합니다.
평균선은 수평이지만 추세선은 수평이 아닙니다. 이는 신호가 선형 추세라는 의미입니다.
변환 영역의 추세 제거 및 저역 통과 필터링
필터링을 통한 평활의 첫 단계는 선형 추세를 제거하는 것입니다. 그렇지 않으면 변환이 고주파수 콘텐츠가 아니라 선형 신호의 주파수 컴포넌트를 표시하게 됩니다.
1. 신호에서 추세를 제거합니다. 새 신호의 기울기와 평균을 다시 계산합니다.
2. 새 함수를 도표화하고 추세선과 평균선을 표시합니다.
평균선과 추세선이 수평입니다. 이는 신호에 선형 추세가 없다는 의미입니다.
3.
dft 함수를 사용하여 신호의 변환을 얻습니다.
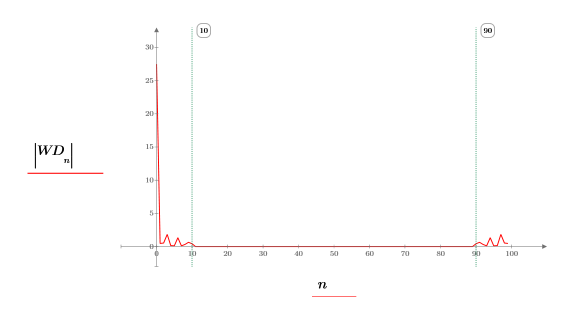
4. 가운데 있는 요소를 소거하고 저역 주파수를 나타내는 시작과 끝만 저장하여 변환을 창에 표시합니다.
5. 창을 씌운 함수를 도표화합니다. 세로 마커를 사용하여 창의 시작과 끝을 표시합니다.
6. idft 함수를 사용하여 역변환을 얻은 다음 추세를 다시 더합니다.
벡터는 요소별로 더해지므로 추세는 단일 더하기 연산자를 사용하여 다시 더해집니다.
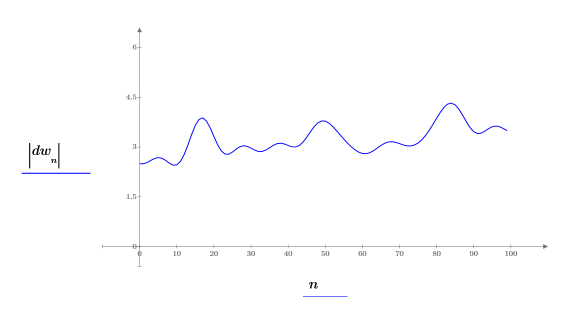
7. dw 함수를 도표화합니다.
추세는 평활화된 함수로 복원되었습니다.
시간-영역 반복 지수 평활
기초값이 적용된 반복 평활 기법을 사용합니다. 반복의 기초값을 구하려면 급수의 시작 부분을 참조하여 고정 값과 추세 값(s 및 b)을 추정합니다.
1.
intercept 및
slope 함수를 사용하여 고정 값과 추세 값을 추정합니다.
2. 평활 상수를 2개 선택합니다. α가 1에 가까울수록 평활화환 곡선이 원래 데이터에 가깝게 지나갑니다.
여기서 P는 원래 시간 급수의 지수 평활 값입니다.
두 기법 비교
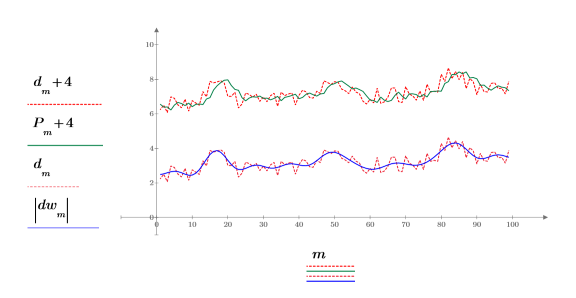
두 가지 평활 기법을 도표화하여 비교합니다. 위쪽 2개 그래프선이 4만큼 떨어져 있으므로 같은 그래프에 표시할 수 있습니다.
• 위쪽 그래프선은 위에서 아래의 순서로 각각 시간 급수, 지수 평활, 시간 급수, DFT로 평활화한 값에 해당합니다.
• 지수 평활은 충분한 점이 평활 계수(a 및 b)로 평균화되기 전에는 데이터를 효과적으로 나타내지 못합니다.
• 워크시트를 다시 계산하고 원래 신호 정의의 일부로 서로 다른 난수가 발생하여 그래프선이 변화하는 방식을 관찰합니다.
• 다시 계산할 때마다 DFT 평활 함수가 지수 평활 함수보다 원래 신호를 더 정확하게 따른다는 것을 확인할 수 있습니다.