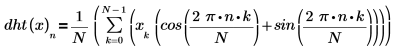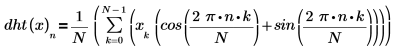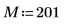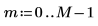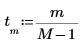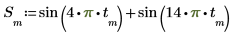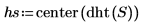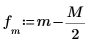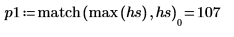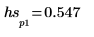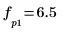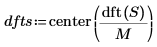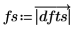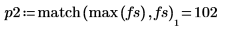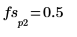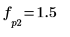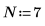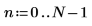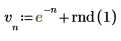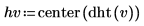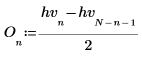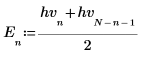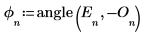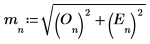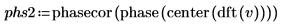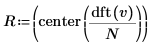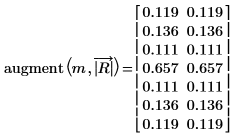例: Hartley 変換
dht関数を使用して、信号の Hartley 変換を求めます。
Hartley 変換の定義和は離散フーリエ変換の和とほぼ同じです。
ここで、N は実数データ配列 x の要素の数です。
正弦波の和
正弦波の和の Hartley 変換を求めて、結果を複素フーリエ変換のマグニチュードと比較します。
1. 要素の数を定義します。
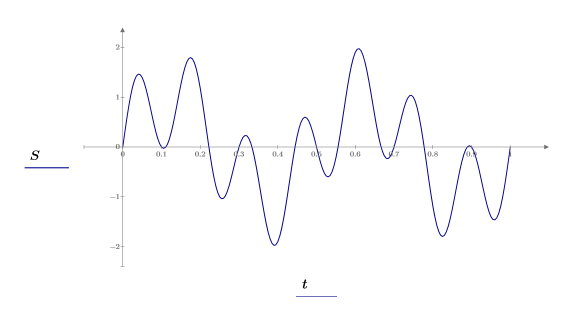
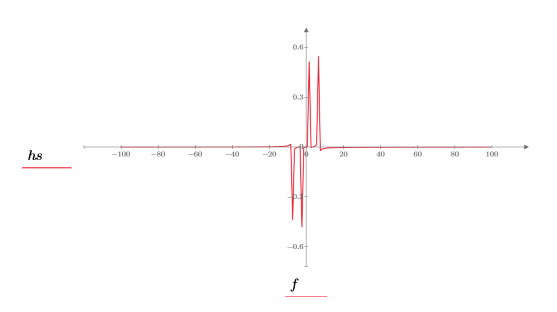
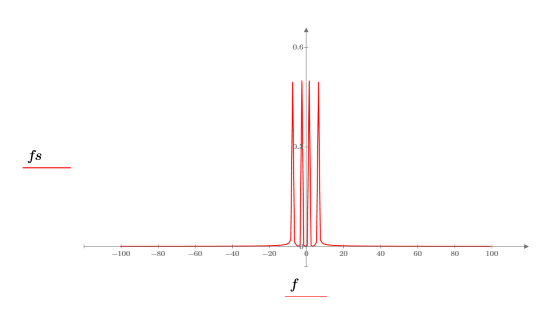
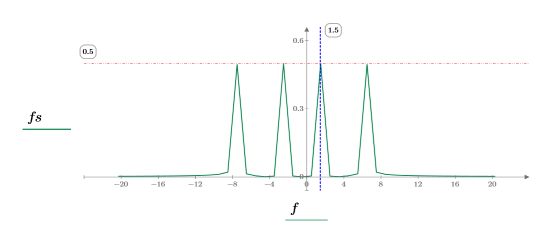
3. 信号をプロットします。
4. dht 関数を使用して 2 つの正弦波によって表される離散周波数を表示してから、
center関数を使用して DC 成分を中央にシフトします。
5.
match関数と
max関数を使用してピークが発生する離散周波数を求め、縦マーカーと横マーカーを使用してこの点にマーク付けします。
6.
dft関数と
center 関数を使用して、離散フーリエ変換を求めて中心を合わせます。
7. DFT の絶対値をプロットします。
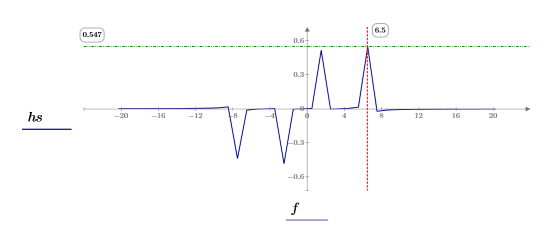
8. match 関数と max 関数を使用して、ピークが発生する離散周波数を求めます。
Hartley 変換から位相とマグニチュードを計算することで、Hartley 変換とフーリエ変換との間の類似性を確認します。これには小さなデータセットを使用できます。
短いノイズ信号
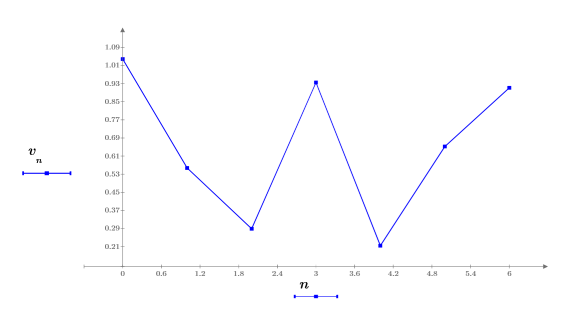
1. 7 つのサンプル点から成る、ノイズを含む入力信号を定義してプロットします。
2. 離散 Hartley 変換を計算して中心を合わせます。
3. 離散 Hartley 変換の奇数部と偶数部を計算します (これらの式は N が奇数であることを前提としています)。
4.
angle関数を使用して、位相ベクトルを計算します。
5. マグニチュードベクトルを定義します。
7.
augment関数を使用して、フーリエ変換で得られた結果に対して位相の結果を比較します。
両方の位相が一致します。
8. dft 関数と center 関数を使用して、マグニチュードベクトルを作成します。
9. augment 関数を使用し、フーリエ変換で得られた結果に対してマグニチュードの結果を比較します。
両方のマグニチュードが一致します。
Hartley 変換とその応用の詳細については、Ronald Bracewell, The Hartley Transform (Oxford University Press) を参照してください。