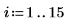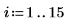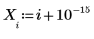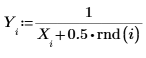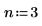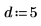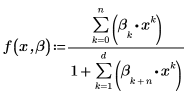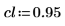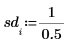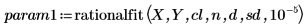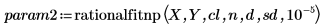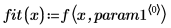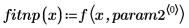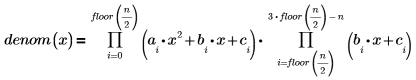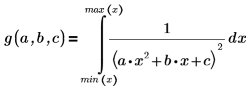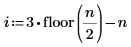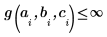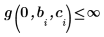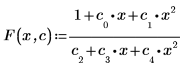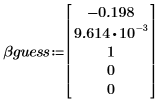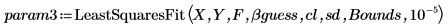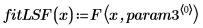例: 有理関数回帰 2
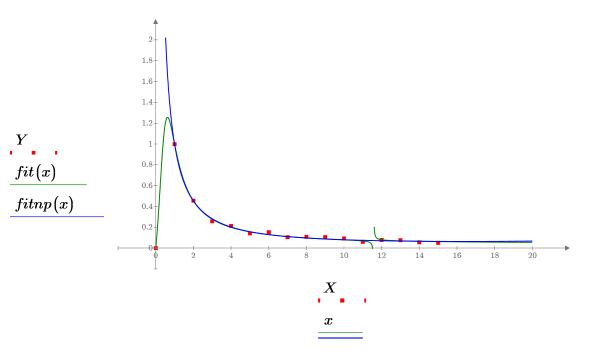
rationalfitnp - 極なし
rationalfit関数と
rationalfitnp関数を使用して有理関数回帰を実行します。
rationalfit 関数ではなく
rationalfitnp 関数を使用した場合、従来の最小二乗問題の解で適合区間内に分母の根があるかどうか調べられます。極がない場合、生成された適合が返されます。極がある場合、非線形最適化問題に追加の制約条件が追加されます。
1. x の逆関数に若干の修正を加えることでデータセットを定義します。
2. 有理関数の分子と分母の次数を指定します。
適合関数の形式は次のとおりです。
3. 信頼限界および標準偏差のベクトルを定義します。
4. rationalfit 関数と rationalfitnp 関数を呼び出します。
param1 と param2 では、1 列目にパラメータが格納され、以降の列には上記で定義した信頼限界における各パラメータの下限と上限が格納されます。
5. データセットと 2 本の回帰曲線をプロットします。
rationalfitnp 関数で極が除去されています。その分母の多項式は次の形式をとります。
極が生じないようにするため、次の制約条件が追加されています。
LeastSquaresFit
rationalfitnp と
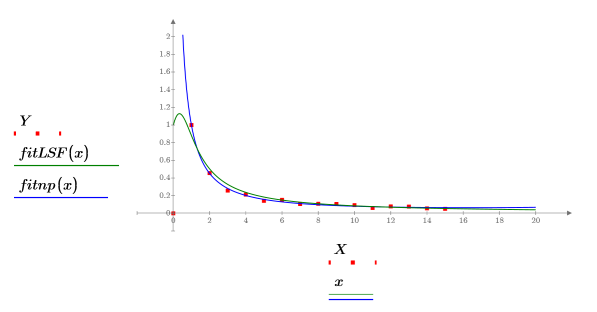
LeastSquaresFitから返された適合曲線を比較します。
LeastSquaresFit 関数は
rationalfitnp と同じアルゴリズムを実行しますが、推定値と信頼限界をパラメータとして指定する必要があります。この関数は、定数項を分母ではなく分子に入れる場合に実行する必要があります。
1. 適合関数を定義します。
2. パラメータの推定値を定義します。
3. パラメータの下限と上限を定義します。
4. LeastSquaresFit 関数を呼び出します。
5. データセット、および rationalfitnp と LeastSquaresFit それぞれから返された適合曲線をプロットします。
| 有理関数適合を実行する前に、データを直線に偏らせる任意のフィルタ手法やデータ変換手法を実行することで、rational 関数での収束速度が大幅に向上し、場合によっては不要な極が取り除かれます。 |