峰态和偏斜度
• kurt(A, B, C, ...) - 返回元素 A, B, C, ... 的峰态。峰态定义如下:
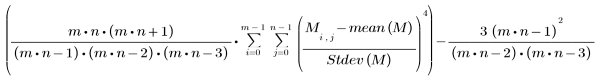
一组值的峰态表示与正态分布相比时,该分布的平坦程度或形成峰值的程度:
值 | 分布形状 |
|---|---|
kurt = 0 | 正态分布 |
kurt > 0 | 相对峰值分布 |
kurt < 0 | 相对平坦分布 |
• skew(A, B, C, ...) - 返回元素 A, B, C, ... 的偏斜度。偏斜度定义如下:
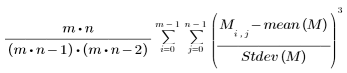
一组值的偏斜度用于测量关于均值的不对称性:
值 | 分布形状 |
|---|---|
skew = 0 | 分布关于均值对称,与正态分布的情形一样。 |
skew > 0 | 分布“尾部”朝正值方向延伸。 |
skew < 0 | 分布“尾部”朝负值方向延伸。 |
自变量
• A, B, C, ... 为标量或数组。对于 kurt,自变量中必须至少有四个元素,对于 skew,必须至少有三个元素。
• M 是从函数自变量 A, B, C, ... 创建的数组。M 的标准差不得为零。