示例:概率分布
使用概率分布函数替代概率分布表。
概率密度
1. 使用 dchisq 函数来计算自由度为 11、在 5.5 处的卡方变量的概率密度:
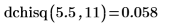
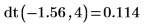
累积概率
1. 使用 pnorm 函数来计算标准正态变量超过 1.0 的概率:
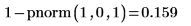
2. 使用 pchisq 函数来计算卡方变量 (自由度为 7) 小于 5.6 的概率:
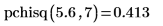
3. 使用 pbinom 函数来计算二项变量 (大小为 15,参数为 0.6) 小于等于 10 的概率。
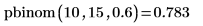
4. 使用 qbinom 函数来计算二项变量 (大小为 15,参数为 0.6) 小于等于 10 的概率。
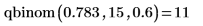
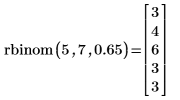
重新计算工作表会导致函数 rbinom 返回新的随机数字集。 |
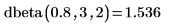
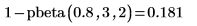
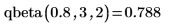
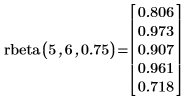
逆累积概率
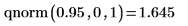
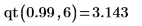
F 分布
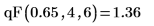
2. 使用 pF 函数来计算自由度为 5 和 7且概率为 0.75 的累积概率分布:
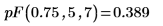
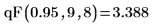
4. 使用 rF 函数来创建由 7 个具有自由度为 2 和 3 的 F 分布的随机数字构成的矢量:

重新计算工作表会导致函数 rF 返回新的随机数字集。 |