示例:乘方回归
使用 genfit 函数
1. 定义数据集。
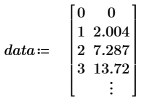
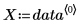
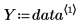
2. 定义拟合函数,其中 A 和 b 未知。
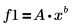
3. 定义函数矢量。
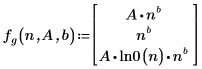
4. 定义估值的矢量。
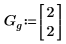
5. 使用 genfit 来求幂函数的系数。
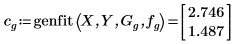
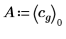
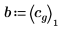
6. 使用系数 A 和 b 来定义函数。
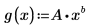
7. 绘制数据点和拟合函数。
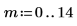
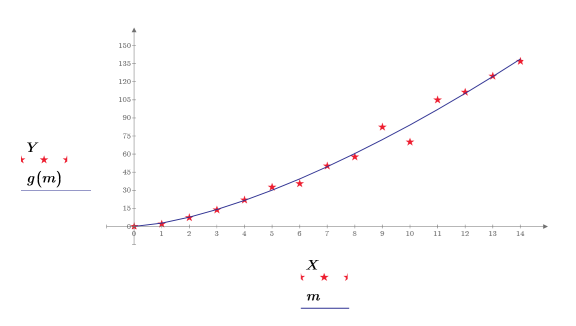
使用 pwrfit 函数
1. 定义拟合函数,其中 a、b 和 c 未知。
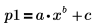
2. 定义估值的矢量。
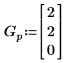
3. 使用 pwrfit 来求幂函数的系数。
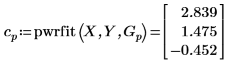
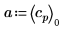
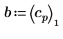
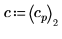
4. 使用系数 a、b 和 c. 来定义函数
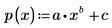
5. 绘制数据点和拟合函数。
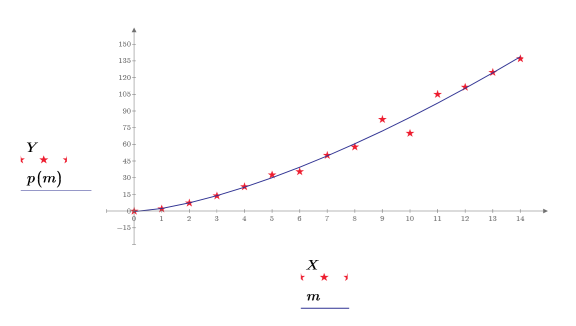
检查拟合度
1. 使用残差图来检查模型与数据的拟合度。
◦ 最大残差值为:
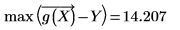
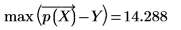
◦ 最小残差值为:
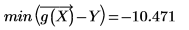
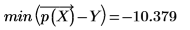
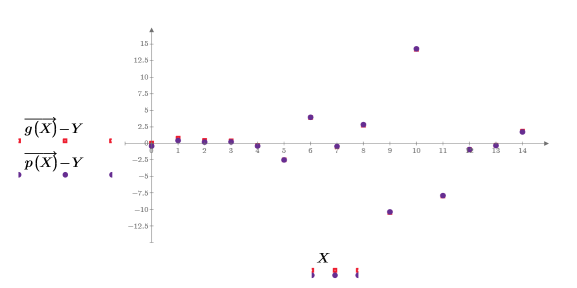
2. 使用 corr 函数计算相关系数。
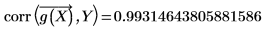
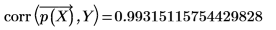
该拟合似乎优于残差图可能显示的情况。
对于大规模存在的数据,特别是随不断增大的 X 值迅速变化的幂数据或指数数据,残差图不一定为确定拟合度的最佳工具。
加权 genfit
使用本地函数来修改根据其他参数代入的 genfit 函数的矢量。
1. 根据数据的标准差来定义加权数据函数。
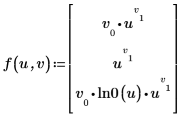
使用参数的矢量输入形式,允许加权函数可简单用于具有任意参数个数的其它类型的拟合函数。
2. 编写一个根据其标准差返回数据 genfit 的程序。

3. 定义标准差的矢量。

4. 倾斜数据集中的其中一个数据点。
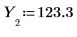
5. 调用程序并将矢量的标准差和估值代入其中。
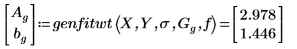
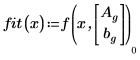
6. 调用不带有权重的 genfit 函数:
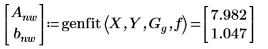
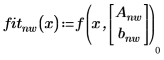
7. 绘制数据及两个拟合函数的图像,并加以比较。
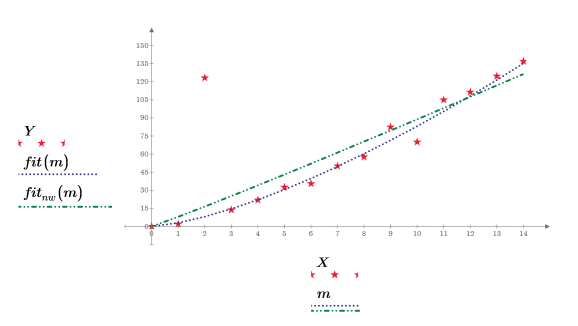
基于标准差的函数可以提供更好的拟合。