非线性回归
genfit(vx, vy, vg, F) - 返回包含参数的矢量,这些参数可使函数 F (具有 x 和 n 参数 u1... un) 最接近 vx 和 vy 中的数据。
genfit 函数采用列文伯格-马夸尔特法的优化版本进行最小化。虽然该方法往往可以提高处理不良估值的速度并降低对其的敏感度,但这一实现可能由于许多局部最小值的问题而无法达到良好的收敛效果,如有理函数。这种处理对于错误的导数矢量非常敏感。
自变量
• vx, vy 为长度相同的实数据值矢量,分别与数据集中的 x 值和 y 值相对应。数据点数必须至少与参数个数相同。
• vg 是参数估值的 n 元素矢量。如果 n = 1,则 vg 为标量。
• F(x, u) 为拟合函数或函数的矢量,其中 x 为自变量,u 为参数矢量或独立参数名称。以下方程为拟合函数的有效表示:
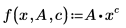
• n 为正整数。对于非矢量化参数,其最多具有九个独立的名称。
改进收敛
要改进 genfit 的收敛和精度 (如有可能),可将 F 表示为下述函数的 n+1 矢量:函数中的第一个条目 F0 是拟合函数 f,而其余条目 F1、F2...Fn 是 f 关于 n 参数的符号偏导数。
根据以上所示表示拟合函数的两种方法,只有对偏导数进行符号求解时,才可以使用 f(x,A,c) 。因此,将 F 表示为函数的矢量时,n 的限值为 9,这样 F 的最大长度便为 10。可通过构建相应偏导数的矩阵并对其进行符号运算来创建矢量 F。
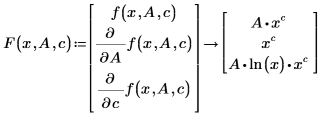
附加信息
• 您应当仅向 genfit 提供拟合函数名称或函数矢量名,而不提供任何自变量。
• 如果使用的拟合函数没有符号参数偏导数,则 genfit 会对参数偏导进行数值计算。如此计算所得结果的精度不及提供符号导数时所得结果的精度,但在某些情况下可能会更方便。
• 如果 genfit 转换失败,可尝试替代列文伯格-马夸尔特方法、其他估值或调整数据,以使所有参数具有类似数量级。
• 列文伯格-马夸尔特优化求解算法对所提供的代数导数中的误差更为敏感。如果此方法失败,请检查导数表达式。
• 与所有数值求解方法一样,非线性问题对于估值也极为敏感。可使用估值绘制拟合函数图像,以便在使用 genfit 前优化估值。