예제: 노이즈 생성 함수
백색 노이즈
whiten 함수는 -0.5 및 0.5 사이에서 균일 분포를 따르는 난수 출력 값을 갖는 N개의 독립적 소스에서 생성된 노이즈를 시뮬레이션합니다.
1. whiten 함수를 사용하여 6개의 독립적 노이즈 소스에 대한 백색 노이즈 함수를 계산합니다.

whiten 함수를 반복해서 계산할 때마다 서로 다른 벡터 요소 집합이 구해집니다.
2. 다소 큰 출력 벡터를 사용합니다.
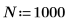
3. 백색 노이즈 함수를 도표화합니다.
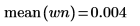
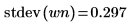
5. 평균의 이론적인 값을 표시한 다음 var 함수를 사용하여 표준 편차를 계산합니다.
도표는 wn 신호의 이론적인 평균이 0임을 보여줍니다. | |
표준 편차는 분산의 제곱근입니다. | 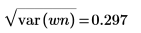 |
6. 계산된 평균 및 표준 편차 값을 이론적인 값과 비교하여 두 값이 크게 차이가 나지 않음을 확인합니다.
가우시안 노이즈
gaussn 함수는 평균 0 및 표준 편차 1의 가우시안 확률 분포를 따르는 x개의 독립적 노이즈 소스를 시뮬레이션합니다.
1. 6개의 독립적 노이즈 소스에 대한 gaussian 노이즈 함수를 계산합니다.

벡터의 요소는 이론적으로 모든 실수 값이 될 수 있지만 대개는 -3 및 +3 사이에 속합니다. F5 키를 눌러 함수를 다시 계산하면 이 사실을 확인할 수 있습니다.
2. 표본 가우시안 시퀀스를 도표화합니다.
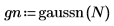
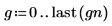
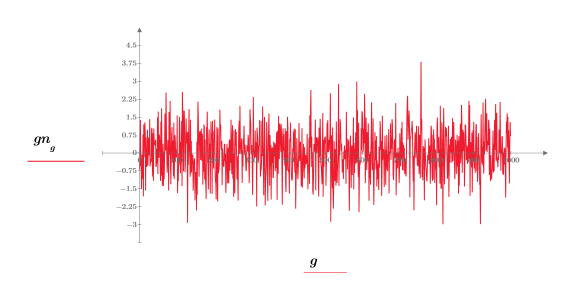
3. 값을 0.05 너비의 20개 빈(bin)으로 그룹화하여 종형 히스토그램 도표에 대한 가우시안 데이터를 준비합니다.
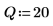
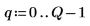
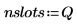
4. 빈(bin) 가장자리를 유지하는 벡터를 정의한 다음 맨 오른쪽 경계를 설정합니다.
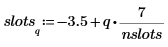
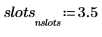
5. hist 함수를 사용하여 히스토그램을 생성한 다음 막대 그래프로 도표화합니다.
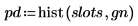
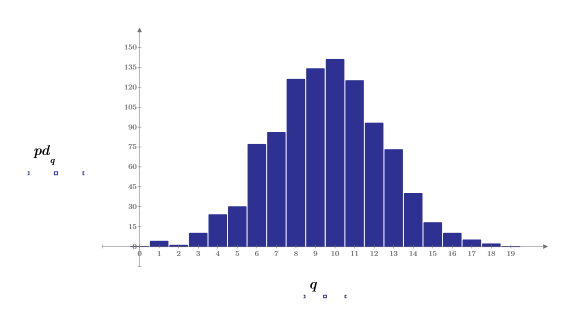
6. 표본의 평균 및 표준 편차를 예상 값인 0 및 1과 비교합니다.
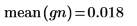
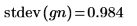
1/f 노이즈
onefn 함수는 Richard Voss가 개발한 알고리즘에 기반한 루틴을 사용하여 1/f 노이즈의 근사치를 계산합니다(Scientific American 1978년 4월호에서 Martin Gardner의 컬럼 참조).
1. onefn 함수를 사용하여 1000개의 점으로 구성된 1/f 벡터를 생성합니다.
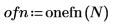
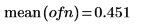
2. 평균 0으로 조정합니다.
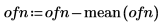
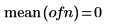
3. 벡터 데이터를 도표화합니다.
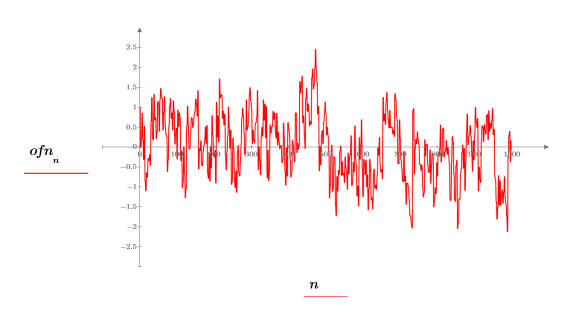
1/f 노이즈는 음악, 뇌파, 날씨, 증시 흐름 등 계층적으로 상호 작용하는 시스템을 비롯한 많은 자연 현상과 인공 현상의 신호에서 발견됩니다. 예를 들어, 록, 재즈, 클래식 등 다양한 스타일의 음악 표본을 디지털화하면 그 파워 스펙트럼이 1/f 노이즈의 분포와 매우 유사하다는 것을 알 수 있습니다.
4. lcorr 함수를 사용하여 각각의 자기상관을 계산하고 이 노이즈의 통계적 구성을 위에서 생성한 백색 노이즈와 비교합니다.
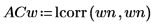
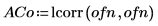
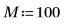
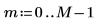
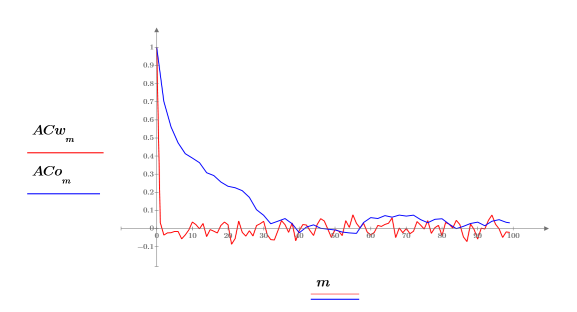
백색 노이즈와 달리 onefn에서 생성된 노이즈는 상관성이 있으며, 이 상관성은 시차가 증가함에 따라 감쇄됩니다.
파워 스펙트럼을 사용한 노이즈 신호 비교
백색 노이즈와 1/f 노이즈 간의 차이를 조사하는 다른 방법은 노이즈의 파워 스펙트럼을 비교하는 것입니다.
1. 20개 주파수 그룹의 50개 빈을 가정합니다.
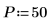
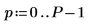
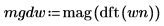
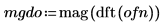
3. 주파수 그룹 전체로 평균화하여 결과를 평활화합니다.
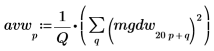
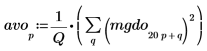
4. 백색 노이즈 스펙트럼을 도표화합니다.
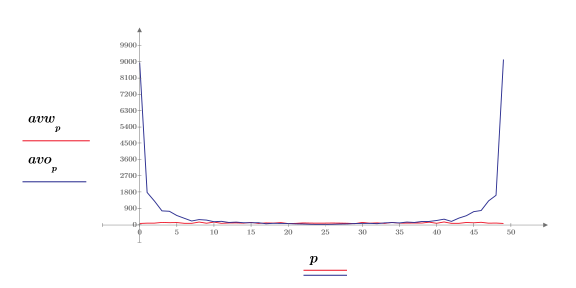
예상대로 백색 노이즈 스펙트럼은 일정합니다. 1/f 근사치의 크기 스펙트럼은 주파수가 증가할수록 빠르게 감소합니다.
5. log 함수를 사용하여 더 많은 정보를 제공하는 크기의 로그를 계산합니다.
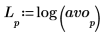
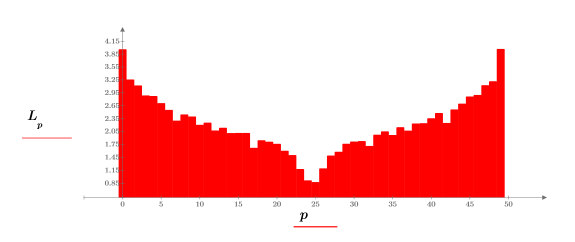
실험
실험으로, 임의의 위상을 갖는 1/f 파워 스펙트럼을 구성하고 역 변환을 사용하여 노이즈 벡터를 구합니다.
1. 스펙트럼의 너비를 정의합니다.
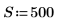
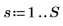
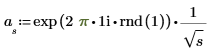
3. 변환의 나머지 절반을 계산합니다(실수 신호인 경우 두 번째 절반은 중점을 기준으로 공액 대칭임).
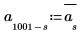
4. 노이즈의 평균을 0으로 설정합니다.
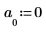
5. idft 함수를 사용하여 역 푸리에 변환을 얻습니다(시간 영역에 대한 변환).
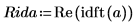
6. 역변환의 실수 값을 도표화합니다.
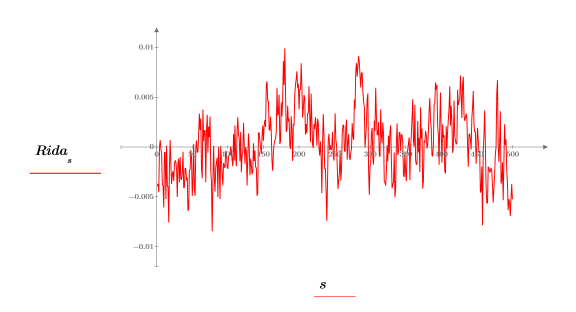
7. lcorr 함수를 사용하여 자기상관 곡선을 계산합니다.
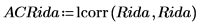
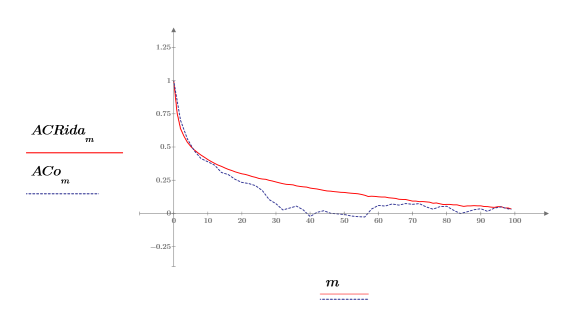
자기상관의 거동은 0에서 상관성이 1.0이고 다른 위치에서는 상관성이 변하는 onefn의 출력과 유사합니다.